How do you solve the triangle given a=8, b=24, c=18?

Question

2091 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-24T16:56:18

Three angles are #color(blue)(hat A = 14.63^@, hat B = 130.75^@, hat C = 34.62^@#

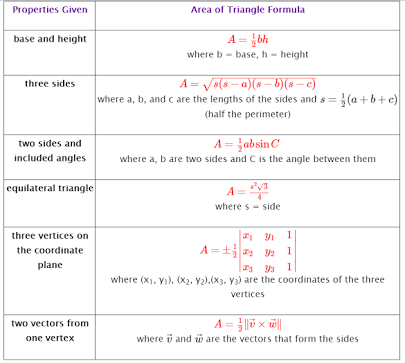
enter image source here

Known three sides. To find the three angles.

#A_t = sqrt (s (s-a) (s-b) (s - c))# where s is the semi perimeter of the triangle.

#s = (8 + 24 + 18)/2 = 25#

#A_t = sqrt(25 * (25-8) (25-24) (25-18))= 54.54#

But #A_t = (1/2) b c sin A#

#:. sin A = (2 * A_t) / (b c) = (2 * 54.54) / (24 * 18) = 0.2525#

#hat A = sin ^-1 0.2525 = 14.63^@#

Similarly,
#hat B = sin ^-1 ((2 * 54.54) / (8*18) )= (180 - 49.24) = 130.75^@# since it is an obtuse angle.

enter image source here

#hat C = sin ^-1 ((2 * 54.54) / (8*24)) = 34.62#