How do you solve the triangle given #C=103^circ, a=3/8, b=3/4#?
1 Answer
Mar 25, 2018
Explanation:
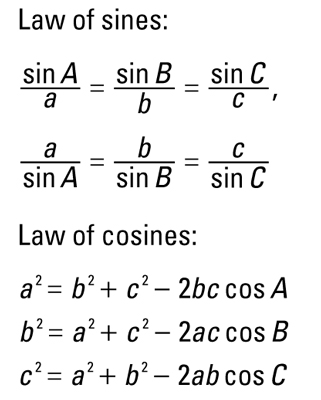
Applying Law of cosines,
Applying Law of sines,
Similarly,
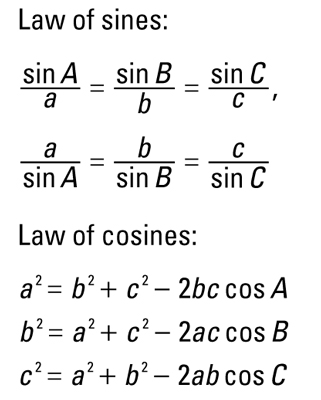
Applying Law of cosines,
Applying Law of sines,
Similarly,