Question

How do you solve the `triangle HJK` given `h=18, j=10, k=23`?

Answer 1

`color(brown)(hat H = 48.47^@, hat J = 24.57^@, hat K = 106.96^@`

`color(indigo)("Area of triangle " A_t = )color(indigo)(86.086 " sq units"`

Explanation:

`"Given : " h = 18, j = 10, k = 23, " To solve the triangle"`

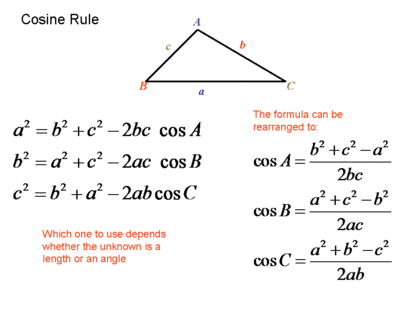
Applying Cosine Rule,

`cos K = (h^2 + j^2 - k^2) / (2 * h * j)`

`cos K = (18^2 + 10^2 - 23^2) / (2 * 18 * 10) = -0.2917`

`hat K = cos ^(-1) -0.2917 = 106.96^@`

Similarly, `cos H = (23^2 + 10^2 - 18^2) / (2 * 23 * 10) = 0.663`

`hat H = cos ^(-1) 0.663= 48.47^@`

Similarly, `cos J = (23^2 + 18^2 - 10^2) / (2 * 23 * 18) = 0.9094`

`hat J = cos ^(-1) 0.9094 = 24.57^@`

`color(indigo)("Area of triangle " A_t = )(1/2) h j sin K = (1/2) * 18 * 10 * sin (106.96^@) = color(indigo)(86.086 " sq units"`