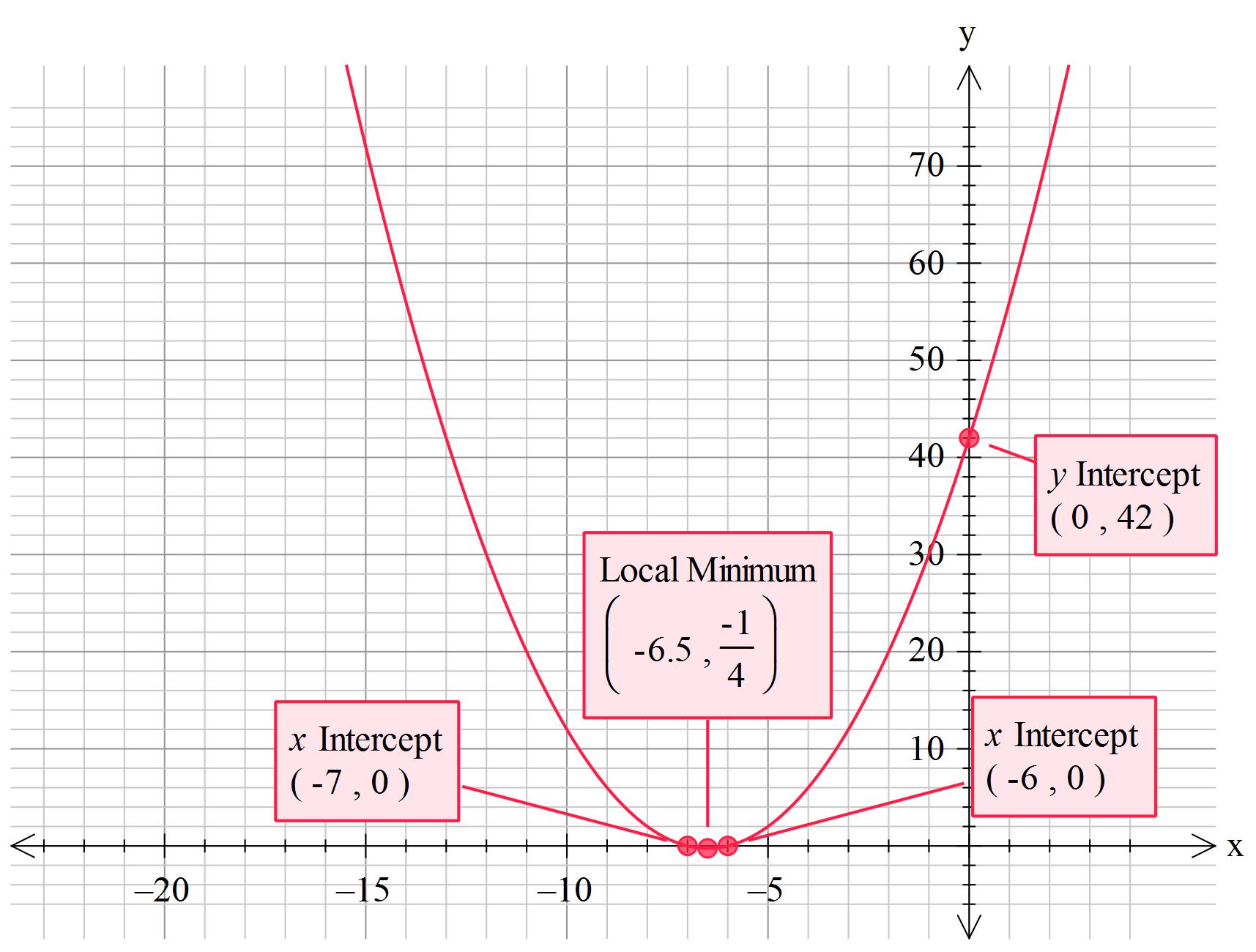
How do you solve using the completing the square method #x ^2 + 13 x + 42 = 0#?
1 Answer
For a very detailed example of method see
http://socratic.org/s/asVauX76
I will let you solve the other bits!
Explanation:
Given:
The process applied introduces an error that is removed by adding the correction factor of
Write as:
Add the correction factor of
Take the power to outside the brackets
Halve the coefficient of
Remove the
The error comes from
So
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Find x-intercepts by substituting 0 for y and solve in the normal way
y-intercept is the constant in the original equation = +42
I will let you solve for the x-intercepts