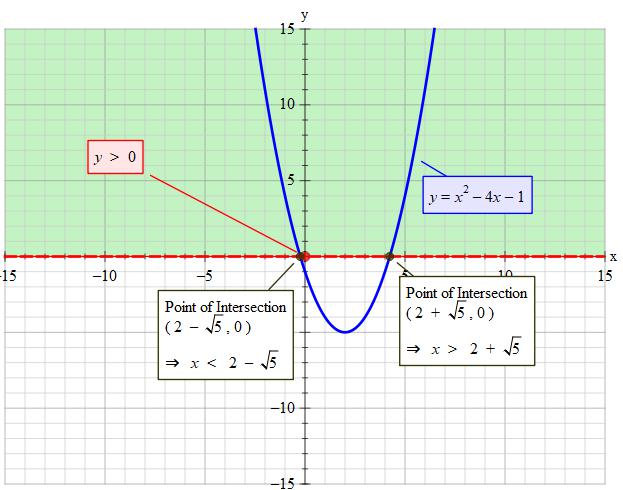
How do you solve #x^2-4x-1 >0#?

Question

3240 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-14T21:55:50

#x>2+-sqrt5#

#x^2-4x-1>0#

Factorise the left into the form #(x+b)^2+c> 0#
Which becomes #(x-2)^2-5>0#

Then move the 5 over to the other side.
Which becomes #(x-2)^2>5#

Then Square root both sides.
Which becomes #x-2 > sqrt5#

Then move the 2 over (#+2#)
Which gives you your answer #x>2+sqrt5#

Square roots have two answers:
#x>2+-sqrt5#

Tony B