How do you solve (x+3)/(3x-6)<=2?
2 Answers
Explanation:
As per the question, we have
 MS Paint
MS Paint
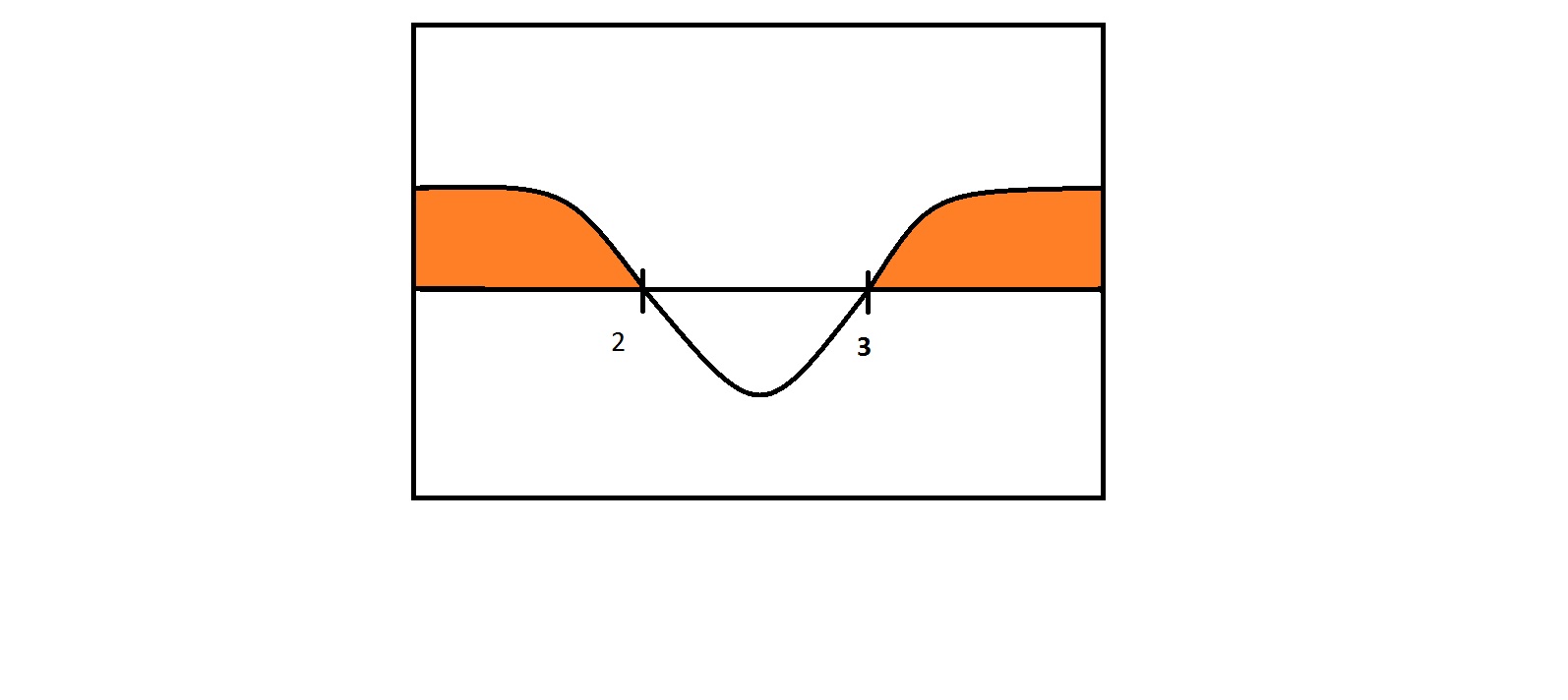
Note : In the image the orange region represents the area on the numberline to which
Hence, the answer.
Explanation:
Multiply by
Factor:
Using signs of brackets:
For:
For:
For:
Solutions in interval notation:
Notice the use of a open interval for 2, this is because for


