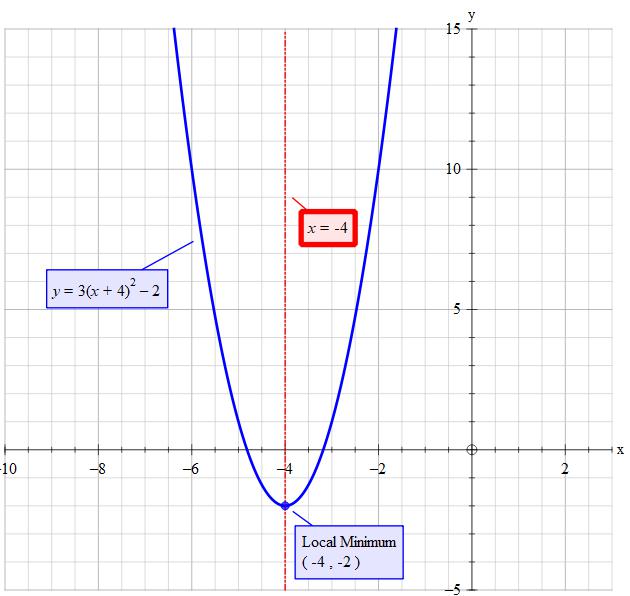
How do you tell whether the graph opens up or down, find the vertex and the axis of symmetry of #y=3(x+4)^2-2#?
2 Answers
See below.
Explanation:
When a quadratic is arranged in the form
From example:
vertex is
axis of symmetry is
If
If
As the
Vertex
So axis of symmetry is
Explanation:
If you expand the brackets and multiply by the three the first term is
As this is positive the graph is of general shape
Suppose it had been negative then in that case the graph would be of form
The given equation format is of type 'completing the square' also known as 'vertex form'.
Vertex