How do you use fundamental identities to find the values of the trigonometric values given sinx = -12/13 and cot > 0?
1 Answer
If cotangent of
Refer to the following image to see the signs of the functions depending on the quadrant.
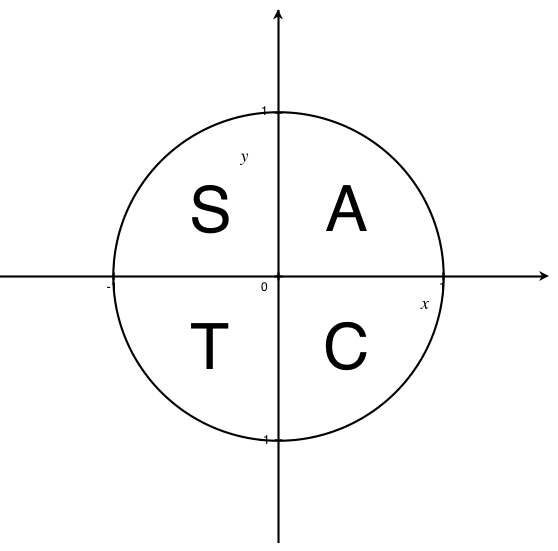
This means that cosine is positive in quadrant IV, all are positive in quadrant I, et cetera, et cetera.
So, we know that sine is negative and tangent is positive. Tangent is positive in quadrants
We can now use pythagorean theorem to determine the adjacent side to
Let the unknown side be
Since cosine is negative in quadrant
We now apply the definitions of the ratios to determine the ratios.
Hopefully this helps!

