How do you use implicit differentiation to find the slope of the curve given #1/(x+1)+1/(y+1)=1# at (1,1)?
2 Answers
The curve has a slope of
Explanation:
Solve for
The slope, or rate of change of the curve is
Explanation:
then
NOTE. What is de difference between
Attached two graphics. The first is associated to
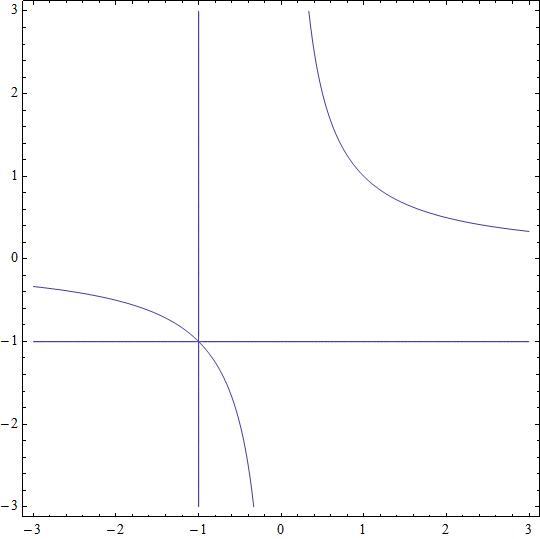
and the second is associated to
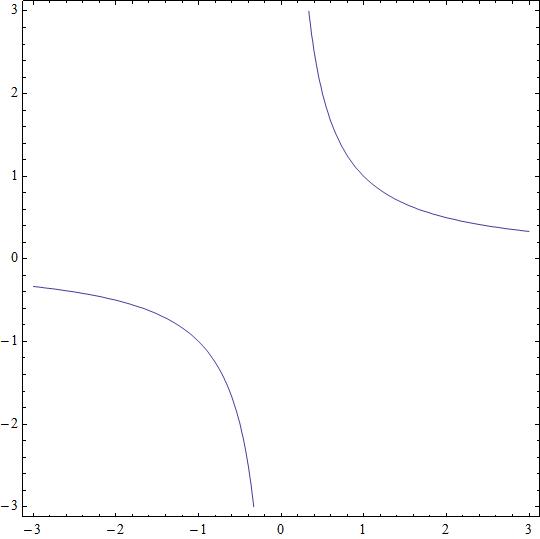
This second graphic is clean, without the singularities in


