How do you use integrals?
1 Answer
Mar 28, 2017
I'll start this off as a collaborative answer:
In the most basic form, integrals are used to represent the area under a curve,
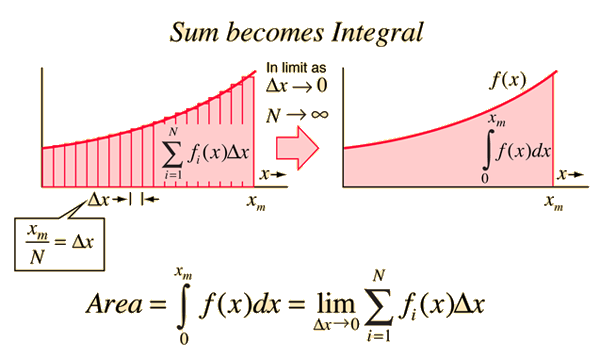
If we attempt to calculate the area under a curve, we can use very thin rectangular strips and form a finite sum that estimates the area between two points. As we take a larger number of thinner strips the estimate will become more accurate.
Calculus deals with the limit of infinitesimals and as we take an infinite number of infinitesimally thins strips we get an exact answer which we represent with an integral sign (here the S shape of the integral sign is designed to remind us that it is a sum.
Thus we represent the area under the curve between
# A = int_a^b \ f(x) \ dx #