How do you use pascals triangle to expand # (d - 5)^6#?
1 Answer
Combine the row of Pascal's triangle that starts with
#(d-5)^6 = d^6-30d^5+375d^4-2500d^3+9375d^2-18750d+15625#
Explanation:
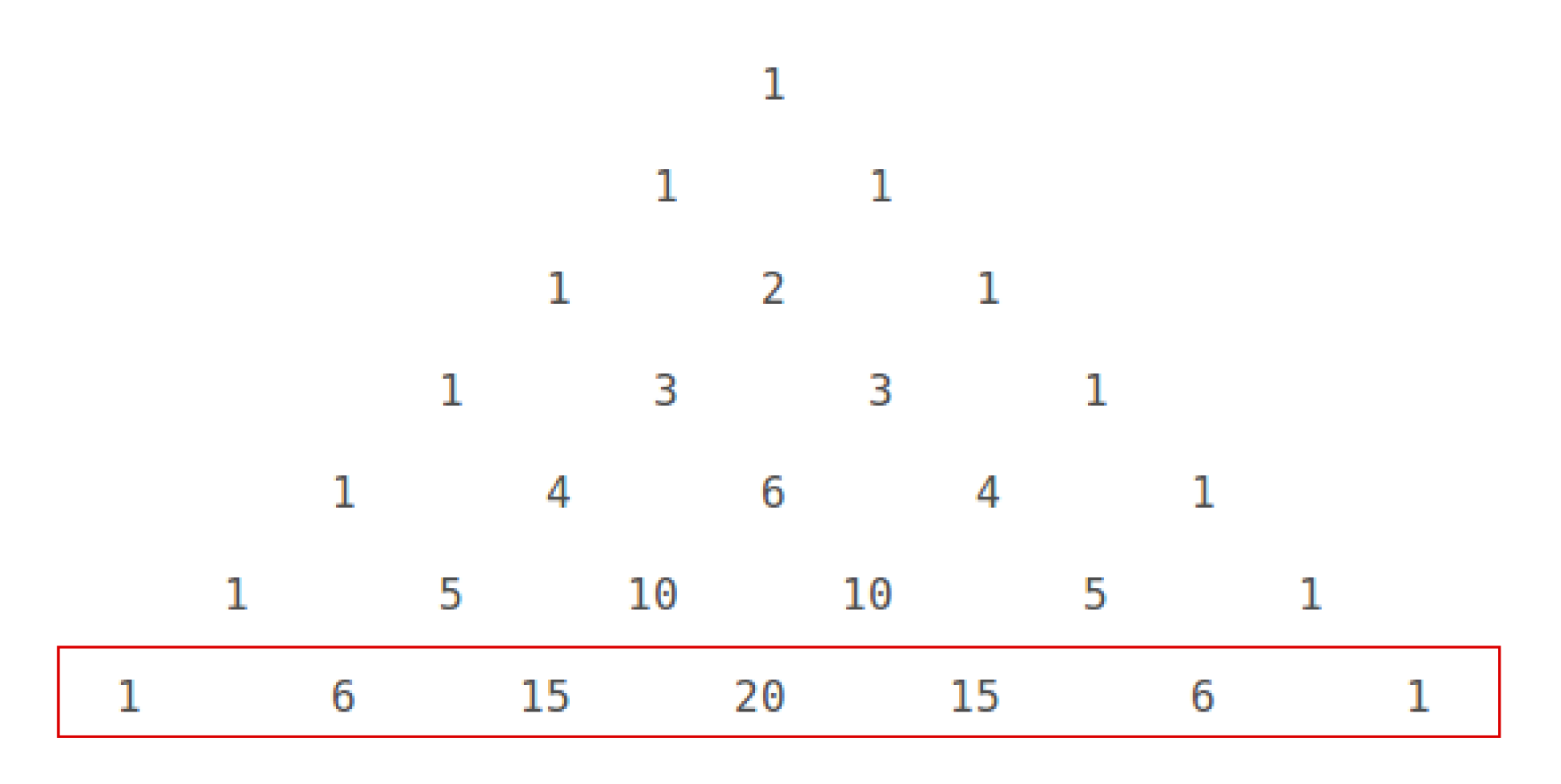
Write out Pascal's triangle as far as the row that begins
Write out this row on its own:
#1# ,#6# ,#15# ,#20# ,#15# ,#6# ,#1#
Write out ascending powers of
#1# ,#-5# ,#25# ,#-125# ,#625# ,#-3125# ,#15625#
Multiply these two sequences together:
#1# ,#-30# ,#375# ,#-2500# ,#9375# ,#-18750# ,#15625#
These are the coefficients we need for our binomial expansion:
#(d-5)^6 = d^6-30d^5+375d^4-2500d^3+9375d^2-18750d+15625#
In general:
#(a+b)^n = sum_(k=0)^n ((n), (k)) a^(n-k) b^k#
where
If you look at the way Pascal's triangle is constructed, with each number being the sum of the two numbers above it, you find that each number is equal to the number of ways that you can reach it starting from the top of the triangle and stepping to the left or right on your way down.
This corresponds to the number of ways that you can choose left and right terms to get a particular power of
#(a+b)^n = stackrel "n times" overbrace((a+b)(a+b)...(a+b))#

