Pascal's Triangle is:
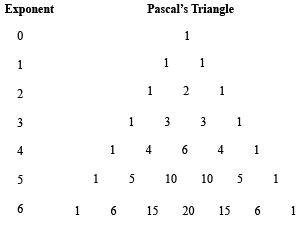
The triangle values for the exponent 6 are:
#color(red)(1)color(white)(.........)color(red)(6)color(white)(.........)color(red)(15)color(white)(.........)color(red)(20)color(white)(.........)color(red)(15)color(white)(.........)color(red)(6)color(white)(.........)color(red)(1)#
Therefore #(d - 5y)^6# is:
#color(red)(1)d^6(-5y)^0 + color(red)(6)d^5(-5y)^1 + color(red)(15)d^4(-5y)^2 + color(red)(20)d^3(-5y)^3 + color(red)(15)d^2(-5y)^4 + color(red)(6)d^1(-5y)^5 + color(red)(1)d^0(-5y)^6 =>#
#(color(red)(1)d^6 * 1) + (color(red)(6)d^5(-5y)) + (color(red)(15)d^4(25y^2)) + (color(red)(20)d^3(-125y^3)) + (color(red)(15)d^2(625y^4)) + (color(red)(6)d^1(-3125y^5)) + (color(red)(1) * 1 *
(15625y^6)) =>#
#d^6 + (-30d^5y) + 375d^4y^2 + (-2500d^3y^3) + 9375d^2y^4 + (-18750dy^5) + 15625y^6) =>#
#d^6 - 30d^5y + 375d^4y^2 - 2500d^3y^3 + 9375d^2y^4 - 18750dy^5 + 15625y^6#

