Question

How do you use pascals triangle to expand `(x^2+5)^6`?

Answer 1

`x^12+30x^10+375x^8+2500x^6+9375x^4+18750x^2+15625`

Explanation:

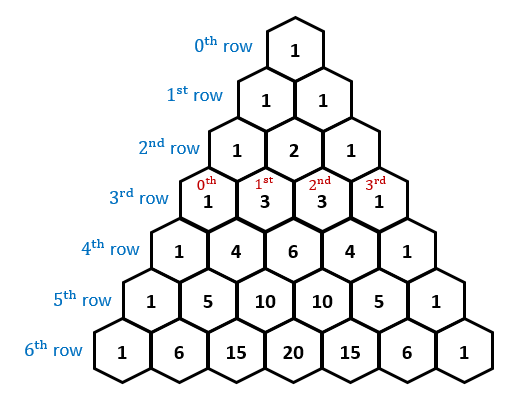
First of all, you'll need to draw out a Pascal's triangle to determine the coefficients of the 6th power.

Then, you expand all `n+1` terms of your expression, where `n` is the binomial power of the expression. In our case here, the binomial power is `6` and there are `6+1=7` terms in the expanded expression.

To expand, simply write out the terms like this:

`(x^2)^6(5)^0+(x^2)^5(5)^1+(x^2)^4(5)^2+(x^2)^3(5)^3+(x^2)^2(5)^4+(x^2)^1(5)^5+(x^2)^0(5)^6`

Then, using the 7 coefficients on the 6th row of Pascal's triangle, multiply each of your 7 terms above from left to right:

`1*(x^2)^6(5)^0+6*(x^2)^5(5)^1+15*(x^2)^4(5)^2+20*(x^2)^3(5)^3+15*(x^2)^2(5)^4+6*(x^2)^1(5)^5+1*(x^2)^0(5)^6`

Once you evaluate the above expression, you should end up with the expanded form:

`x^12+30x^10+375x^8+2500x^6+9375x^4+18750x^2+15625`