Question

How do you use `tantheta=4` to find `costheta`?

Answer 1

`cos theta = pm 1/sqrt{17}`

Explanation:

You could use the identity `sec^2 theta = tan^2theta +1` to find that in this case `sec^2 theta = 16+1=17`, so that `sec theta = pm sqrt{17}` Since `sec theta = 1/cos theta`, this tells us that

`cos theta = pm 1/sqrt{17}`

Unfortunately the sign of `cos theta` can not be found from the value of `tan theta`. Since `tan theta` is positive in this case, the angle `theta` may lie in either the first or the third quadrant. If the angle is in the first quadrant, then `cos theta = 1/sqrt{17}`. If, on the other hand, it is in the third quadrant, then `cos theta = -1/sqrt{17}`

Answer 2

`cos(theta)=1/sqrt(17)color(white)("xxx")"or"color(white)("xxx")cos(theta)=-1/sqrt(17)`

Explanation:

If `tan(theta)=4`
then the ratio of the opposite side to the adjacent side is `4:1`

Two possibilities exist depending upon whether `theta` is in Quadrant I or Quandrant III; as indicated below:

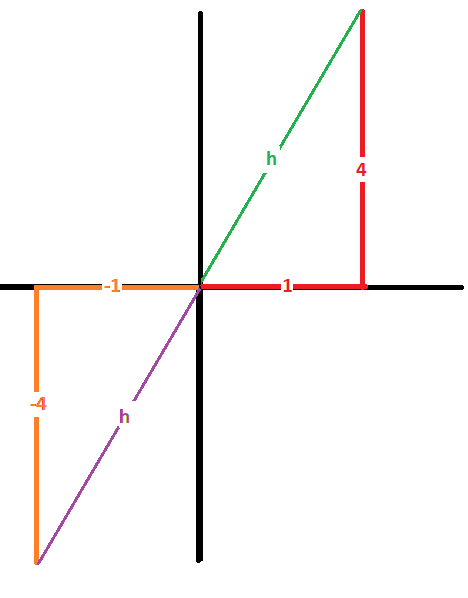
In either case the relative length of the hypotenuse is given by the Pythagorean Theorem as
`color(white)("XXX")h=sqrt(4^2+1^2)=sqrt(17)`

Since
`color(white)("XXX")cos(theta)="adjacent"/("hypotenuse")`
for this case
`color(white)("XXX")cos(theta)=1/sqrt(17)color(white)("xx")"or"color(white)("xx")(-1)/sqrt(17)`