Question

How do you use the midpoint rule to estimate area?

Answer 1

show below please.

Explanation:

A good way to approximate areas with rectangles is to make each rectangle cross the curve at the midpoint of that rectangles top side.
A midpoint sum is a much better estimate of area than either a left-rectangle or right-rectangle sum.

The figure below shows you why it is better:

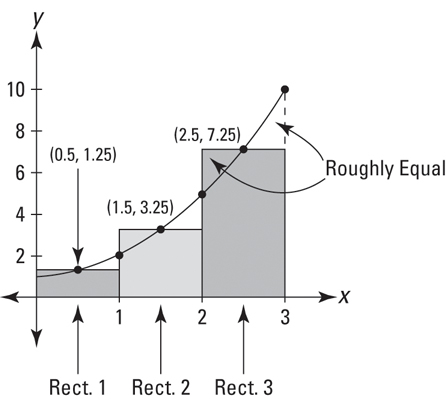
You can see in the figure that the part of each rectangle that’s above the curve looks about the same size as the gap between the rectangle and the curve.
A midpoint sum produces such a good estimate because these two errors roughly cancel out each other.

`"Midpoint Rectangle Rule"`

You can approximate the exact area under a curve between a and b

`A=int_a^by*dx`

with a sum of midpoint rectangles given by the following formula.

In general, the more rectangles, the better the estimate:

`A_"Midpoint"=(b-a)/n[f((x_0+x_1)/2)+f((x_1+x_2)/2)+...+f((x_n-1+x_n)/2)]`

Where, n is the number of rectangles

`width=(b-a)/2`

is the width of each rectangle, and the function values are the heights of the rectangles.