Question

How do you use the Pythagorean Theorem to determine if the following triangle with sides a, b, & c is a right triangle: a=5, b=10, c=15?

Answer 1

`c^2 != a^2 + b^2`, therefore, this cannot be a right triangle.

Explanation:

The Pythagorean Theorem applies to right angle triangles, where the sides `a` and `b` are those which intersect at right angle. The third side, the hypotenuse, is then `c`

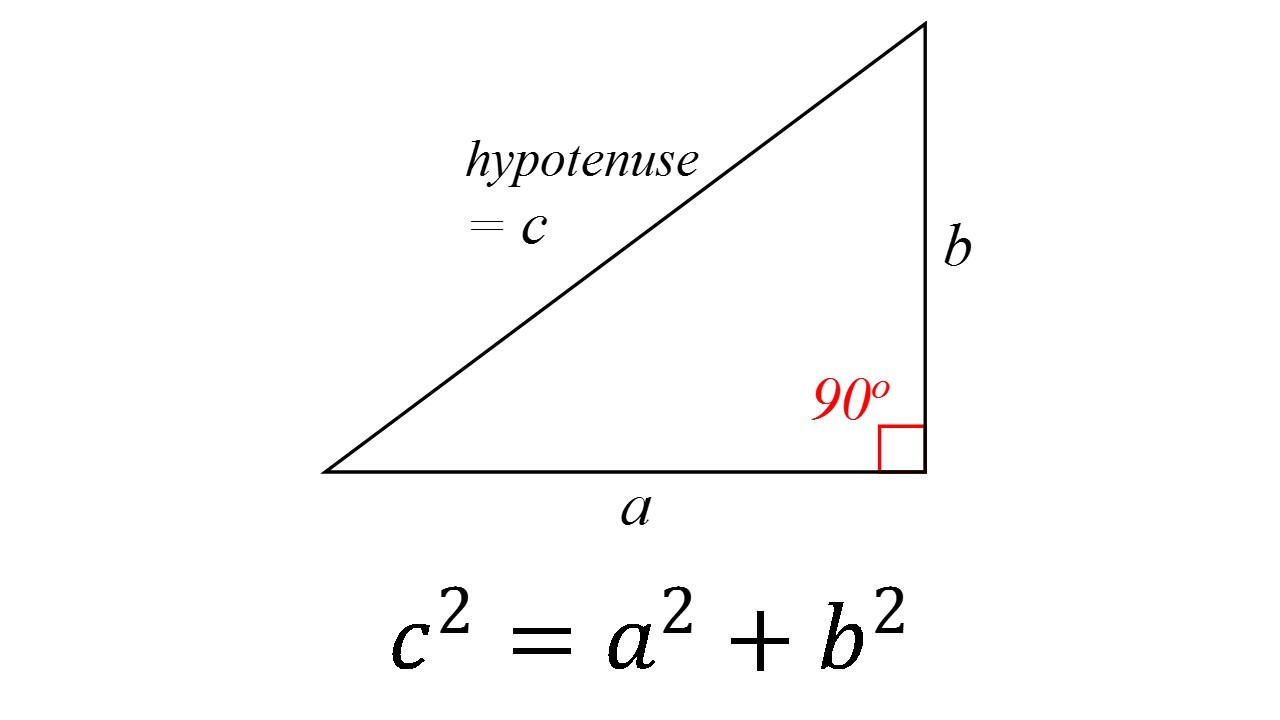
To test whether the given lengths of sides create a right triangle, we need to substitute them into the Pythagorean Theorem - if it works out then it is a right angle triangle:

`c^2 = a^2 + b^2`

`15^2 != 5^2+10^2`
`225 != 25+100`
`225 != 125`

In reality, if `a=5` and `b=10` then `c` would have to be

`c^2 = 125`
`c =sqrt(125) = 5sqrt(5)~= 11.2`

which is smaller than the proposed value in the question. Therefore, this cannot be a right triangle.