How do you use the rational roots theorem to find all possible zeros of #f(x) = 3X^5 - 2X^2 + 16X - 2#?
1 Answer
Use a numerical method to find:
#x ~~ 0.12701#
#x ~~ 1.03966+-0.998855i#
#x ~~ -1.10317+-1.14378i#
Explanation:
By the rational roots theorem, any rational zeros of
That means that the only possible rational zeros of
#+-1/3# ,#+-2/3# ,#+-1# ,#+-2#
You can substitute each of these into the formula for
So this quintic has no rational zeros.
By the fundamental theorem of algebra it does have exactly
In addition, since its coefficients are Real, any non-Real Complex zeros must occur in Complex conjugate pairs.
Typically for a quintic, the zeros of this particular one are not expressible in terms of
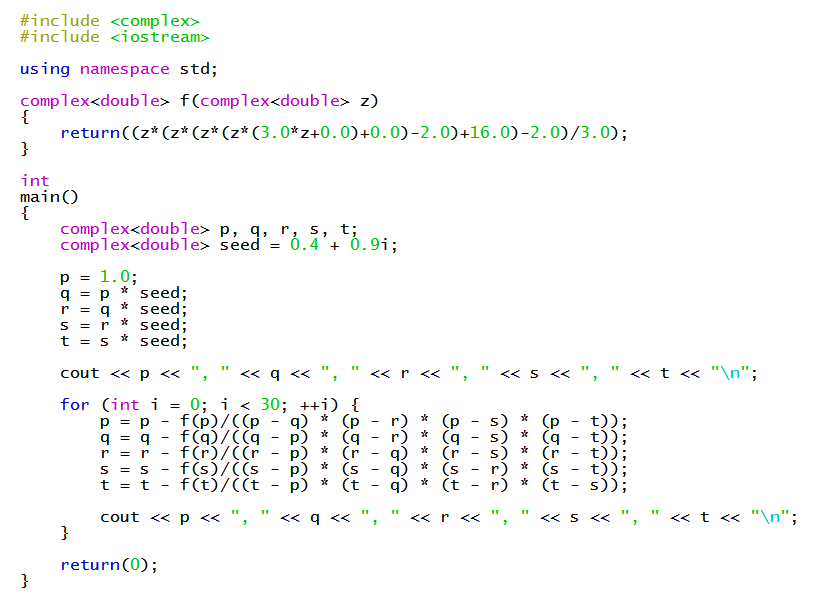
About the best we can do is find numeric approximations using a method like Durand-Kerner. See https://socratic.org/s/avyDEG5X for a fuller explanation, but the Durand-Kerner algorithm finds approximations for all
The results I found were:
#x ~~ 0.12701#
#x ~~ 1.03966+-0.998855i#
#x ~~ -1.10317+-1.14378i#
Here's the C++ program I used to find them: