How do you write a nuclear equation for the alpha decay of #"_62^148Sm#?
1 Answer
Explanation:
The thing to remember about alpha decay is that it occurs when the nucleus of a radioactive nuclide emits an alpha particle,
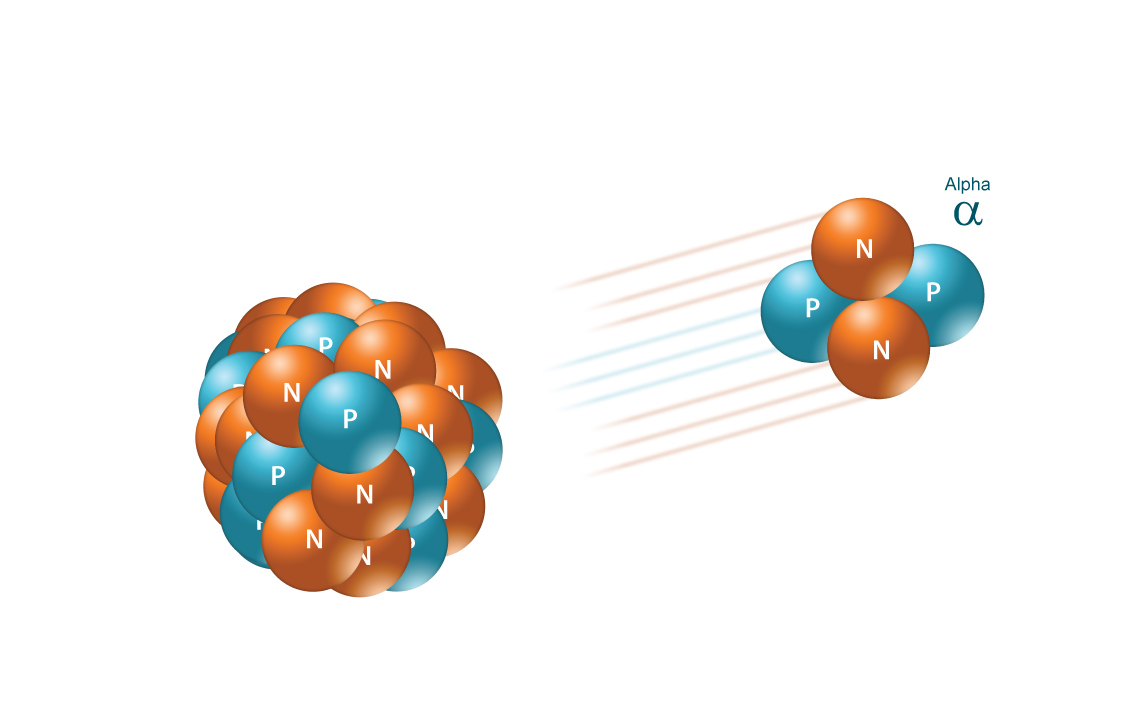
Simply put, an alpha particle contains
Therefore, you can use isotopic notation to write the alpha particle using its atomic number of
#""_2^4alpha#
You can now set up the nuclear equation that describes the alpha decay of samarium-148
#""_ (color(white)(1)color(blue)(62))^color(orange)(148)"Sm" -> ""_color(blue)(Z)^color(orange)(A)"X" + ""_color(blue)(2)^color(orange)(4)alpha#
In order to find the identity of the daughter nuclide, use the fact that mass and charge are conserved in a nuclear equation
#color(orange)(148 = A + 4)" " -># conservation of mass
#color(white)(1)color(blue)(62 = Z + 2)" " -># conservation of charge
Solve to find the values of
#148 = A + 4 implies A = 144#
#color(white)(1)62 = Z + 2 implies Z = 60#
Grab a periodic table and look for the element which has the atomic number equal to
The balanced nuclear equation that describes the alpha decay of samarium-148 will thus be
#color(darkgreen)(ul(color(black)(""_ (color(white)(1)62)^148"Sm" -> ""_ (color(white)(1)60)^144"Nd" + ""_2^4alpha)))#

