How do you write #abs(x^2 +x -12)# as a piecewise function?
1 Answer
Use the definition:
Find the points where the quadratic is zero to simplify the restrictions and add pieces as needed.
Explanation:
Given
Use the definition,
Find the x values for
Factor:
This means that
Modify the restriction for the first piece to be
Modify the restriction for the middle piece to be
Here is a graph of
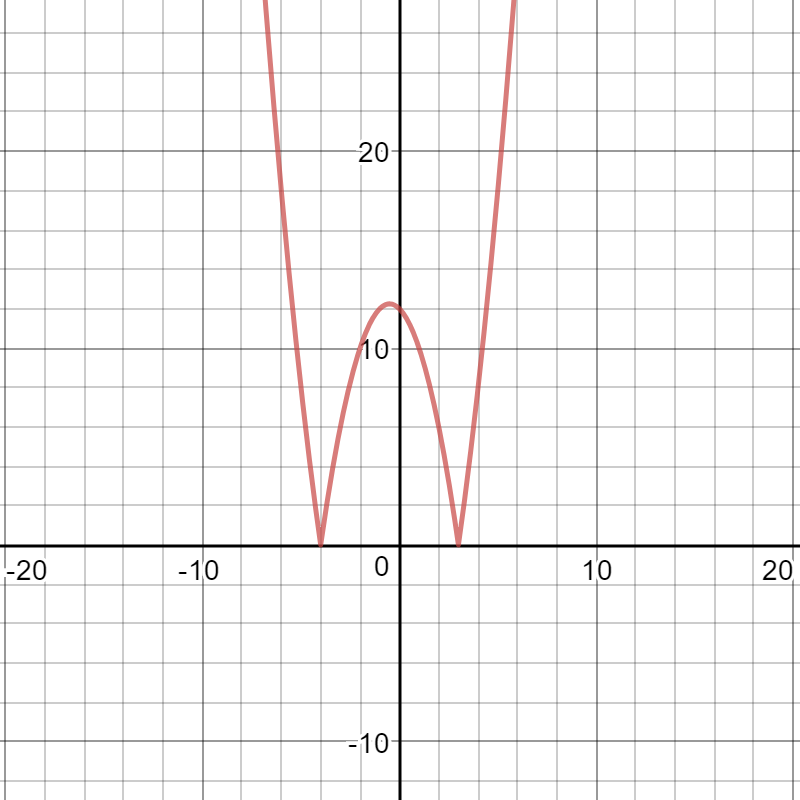
Here is a graph of the piece-wise function
with each piece in a different color: