How do you write an equation for a circle with Point A is (4, -2) Point B is (10,6) as diameters?
1 Answer
We must first find the length of the diameter and the center of the circle.
The center is an equal distance from all points inside a circle. Therefore, we can use the midpoint formula
The center will therefore be at
Now for the length of the diameter.
This can be found by using the distance theorem, a simple variation on pythagorean theorem.
Hence, the diameter measures
Solving for r:
Now that we know our radius, we can substitute what we know into the equation of the circle, of the form mentioned above:
Here is the graph of this relation (note: it's not a function, since every value of x is not only with one value of y)
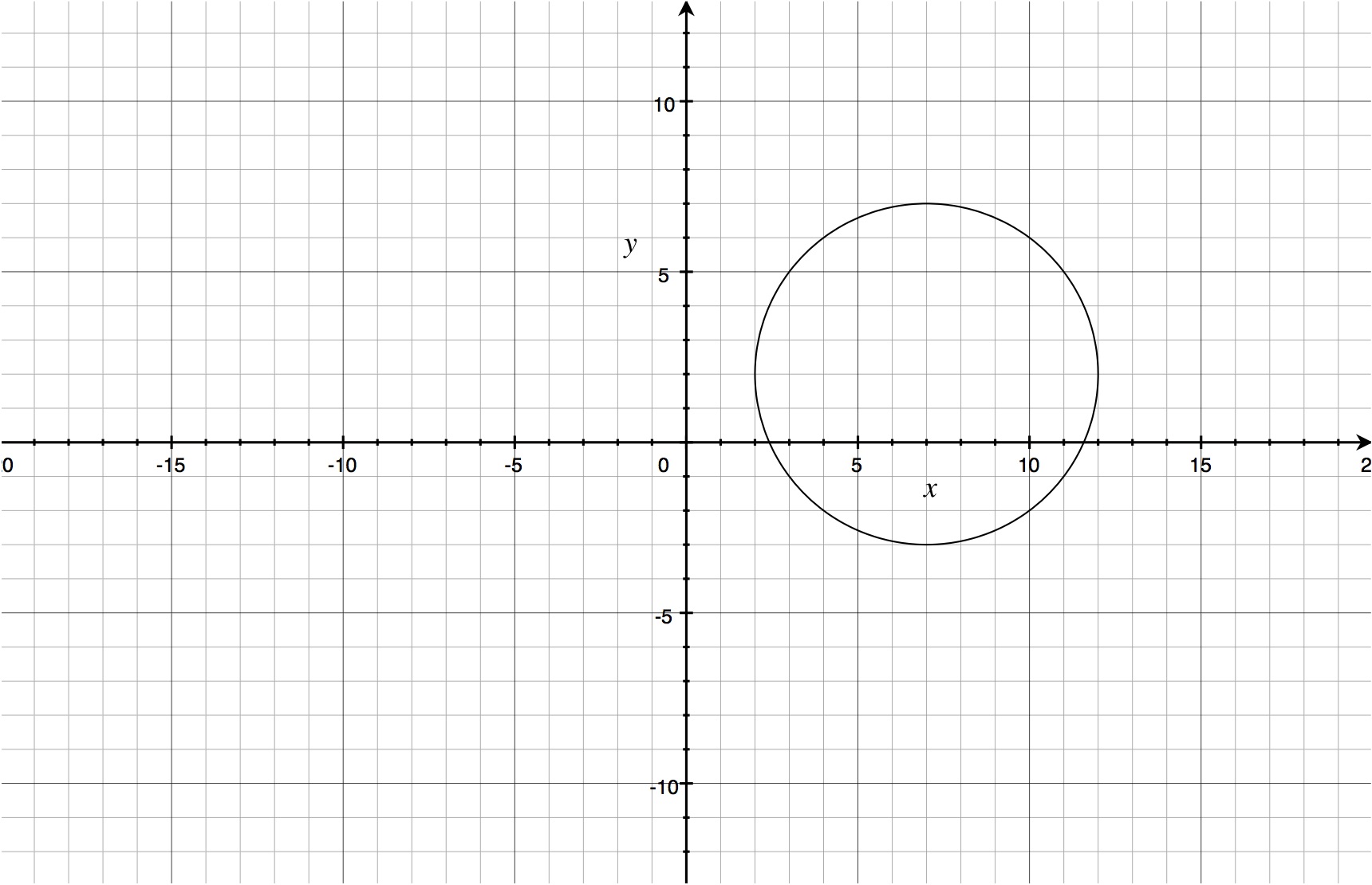
Practice exercises:
- Determine the equation of the circle who's diameter ends at the points
#(-1, -4)# and#(3, -5)# .
Hopefully this helps, and good luck!

