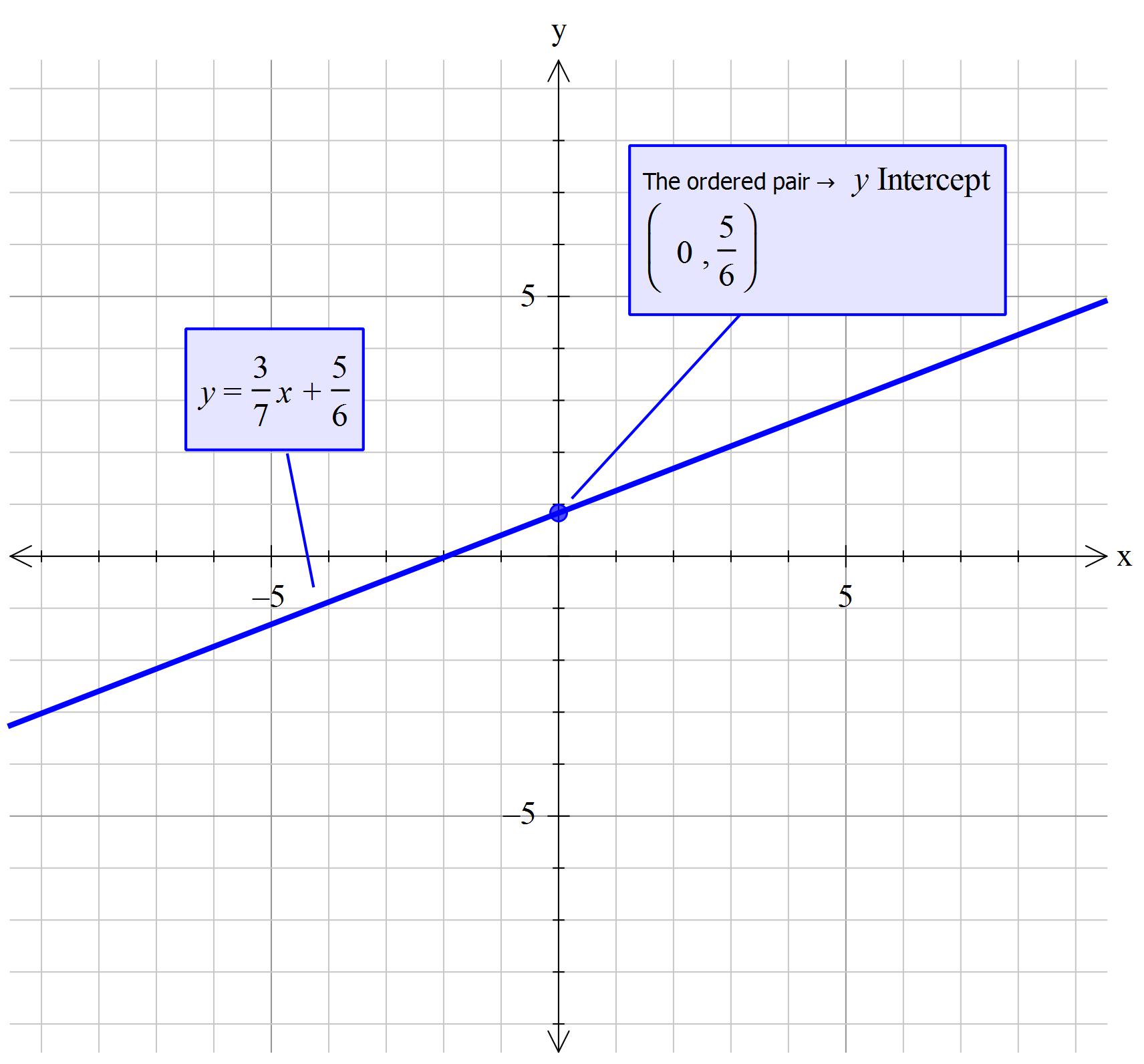
How do you write an equation of a line given slope is 3/7 and the ordered pair is (0, 5/6)?

Question

How do you write an equation of a line given slope is 3/7 and the ordered pair is (0, 5/6)?

3 Answers

Impact of this question

3949 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-15T15:17:13

$y = \frac{3}{7} x + \frac{5}{6}$ $y=3/7x+5/6$

Explanation:

$Step 1$ $color(red)("Step 1")$
The general equation of a straight line is: $y = m x + c$ $y=mx+c$

Where $m$ $m$ is the gradient and $c$ $c$ is a constant which is also the y-intercept.

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
$Step 2$ $color(red)("Step 2")$

We are told that the gradient (slope) is $\frac{3}{7}$ $3/7$ so by substituting this for $m$ $m$ we have

$y = \frac{3}{7} x + c$ $y=3/7x+c$

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

$Step 3$ $color(red)("Step 3")$

We are given a condition where this equation is true. We are told that it passes through the point $(x, y) \to (0, \frac{5}{6})$ $(x,y)->(color(blue)(0,5/6))$

So we van substitute for both $x$ $x$ and $y$ $y$ to determine the value of $c$ $c$ .

$y = \frac{3}{7} x + x \to \frac{5}{6} = \frac{3}{7} (0) + c$ $color(brown)(y=3/7x+x" "->" "color(blue)(5/6)=3/7(color(blue)(0))+c)$

But $\frac{7}{7} \times 0 = 0$ $7/7xx0=0$ giving:

$\frac{5}{6} = c$ $5/6=c$

Thus the finished equation is:

$y = \frac{3}{7} x + \frac{5}{6}$ $y=3/7x+5/6$

Tony P Tony P

Answer 2 · 2016-07-15T15:26:52

$y = \frac{3}{7} x + \frac{5}{6}$ $y = 3/7x +5/6$

Explanation:

There is a nifty formula for the equation of a line which applies in just such a case where we are given the slope and one point.

Using this formula requires only ONE step with substitution and some easy simplifying. Works like a dream...

$y - y_{1} = m (x - x_{1}) m = slope and (x_{1}, y_{1}) is a point$ $y-y_1 = m(x-x_1)" m = slope and "(x_1,y_1)" is a point"$

$y - \frac{5}{6} = \frac{3}{7} (x - 0)$ $y -5/6 = 3/7(x-0)$

$y = \frac{3}{7} x + \frac{5}{6}$ $y = 3/7x +5/6$

However, in this particular case, no working was required at all.

The slope, m is given as $\frac{3}{7}$ $3/7$ and the point given happens to be the y-intercept because the $x -$ $x-$ value is 0. So $c = \frac{5}{6}$ $c = 5/6$

$y = m x + c \Rightarrow y = \frac{3}{7} x + \frac{5}{6}$ $y = mx + c rArr y = 3/7x +5/6$

Answer 3 · 2016-07-15T15:27:13

Alternative approach

$y = \frac{3}{7} x + \frac{5}{6}$ $y=3/7x+5/6$

Explanation:

Let the slope (gradient) be $m$ $m$

The gradient (slope) the change in up or down for a given change in along.

$m = \frac{Change in y}{Change in x} = \frac{3}{7}$ $m=("Change in y")/("Change in x") = 3/7$

Let given point be $P_{o} \to (x_{o}, y_{o}) = (0, \frac{5}{6})$ $P_o->(x_o,y_o) = (0,5/6)$

Let any other point be $P_{i} \to (x_{i}, y_{i})$ $P_i->(x_i,y_i)$

Then $m = \frac{Change in y}{Change in x} \to \frac{y_{i} - y_{o}}{x_{i} - x_{o}} = \frac{y_{i} - \frac{5}{6}}{x_{i} - 0} = \frac{3}{7}$ $m=("Change in y")/("Change in x") -> (y_i-y_o)/(x_i-x_o) = (y_i-5/6)/(x_i-0) = 3/7$

$y_{i} = \frac{3}{7} x_{i} + \frac{5}{6}$ $y_i=3/7x_i+5/6$
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
$y = \frac{3}{7} x + \frac{5}{6}$ $y=3/7x+5/6$

Science

Math

Humanities

... and beyond

How do you write an equation of a line given slope is 3/7 and the ordered pair is (0, 5/6)?

3 Answers

Explanation:

Explanation:

Explanation:

Related questions

Impact of this question