How do you write an equation of #y=sinx# with pi/2 units to the right and 3.5 units up?
1 Answer
Nov 3, 2017
Explanation:
Subtracting
Adding a constant to
So:
See graphs:
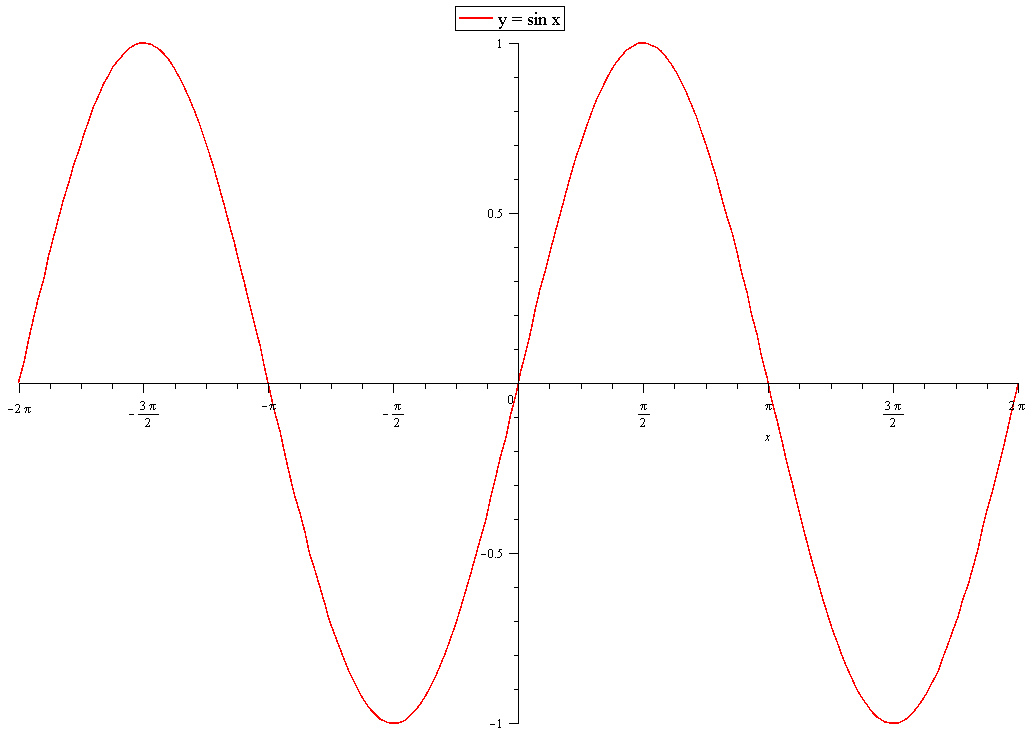
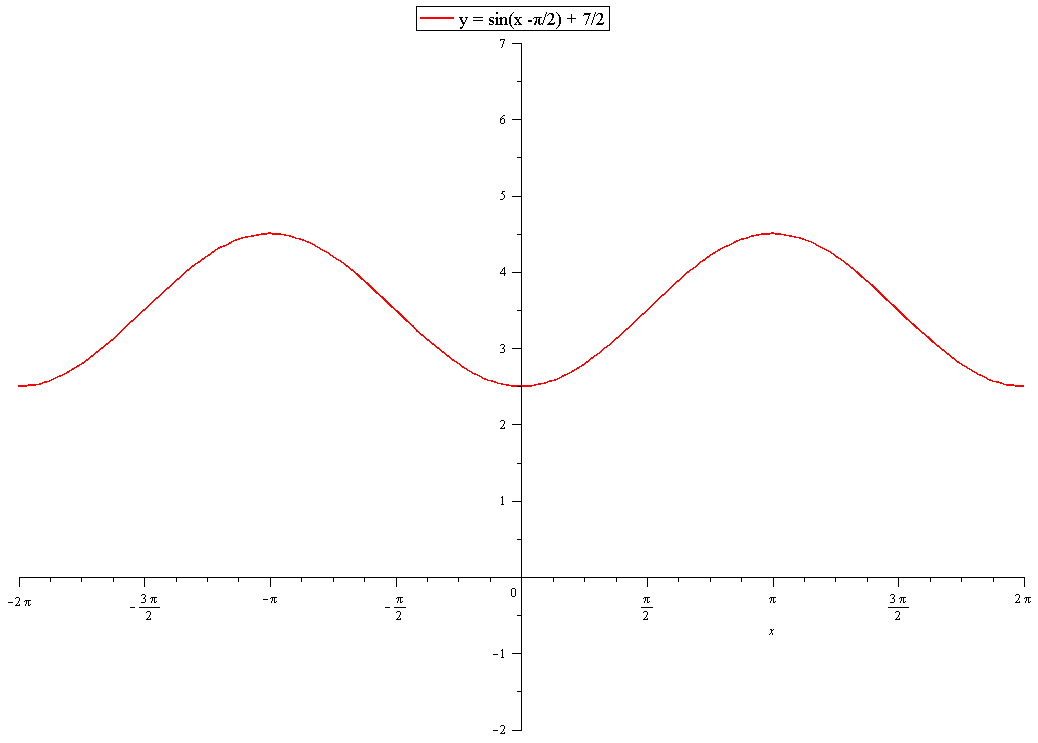
Subtracting
Adding a constant to
So:
See graphs:

