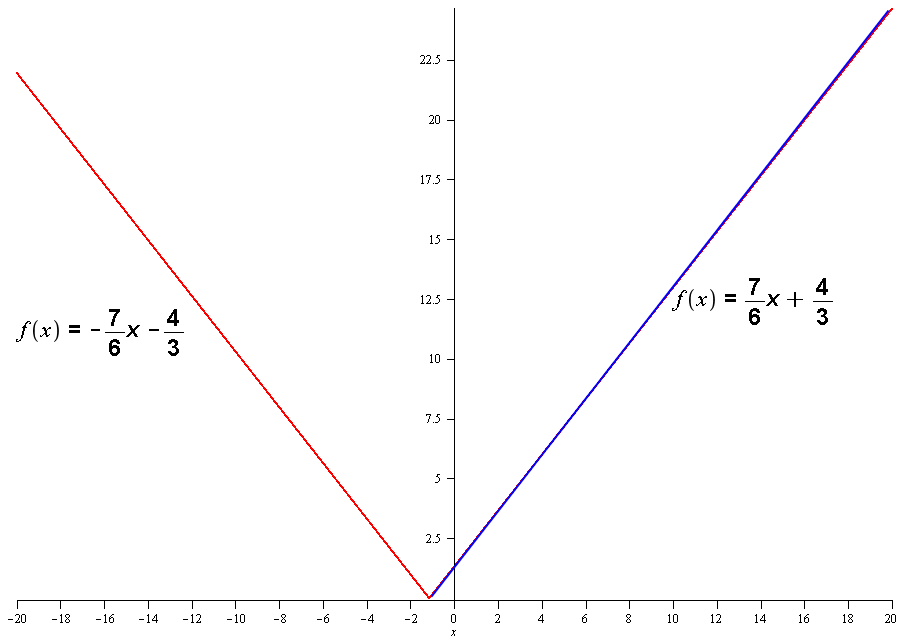
How do you write #f(x)= |7/6x+4/3|# as a piecewise function?

Question

1561 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-24T18:22:38

See below.

The definition of absolute value.

#|a|=acolor(white)(8888888)# If and only if #color(white)(8888888)a>=0#

#|a|=-acolor(white)(8888)# If and only if #color(white)(8888888)a<0#

First we recognise that if #7/6x+4/3<0# , we have #-(7/6x+4/3)#

And if #7/6x+4/3>=0color(white)(88)# we have #color(white)(888)(7/6x+4/3)#

#7/6x+4/3<0=>x<-8/7#

#7/6x+4/3>=0=>x<-8/7#

So piecewise we have:

#f(x)=[(-7/6x-4/3 , ->x<-8/7),(,),(7/6x+4/3,->x>=-8/7)]#

enter image source here