#n#: the principal quantum number relates to the size of the orbital
#l#: the angular quantum number relates the shape of the orbital and ranges from #0# to #n-1#
#m_l#: the magnetic quantum number relates the spatial orientation of the orbital and ranges from #[-l,l]#
#m_s#: the magnetic spin quantum number relates the spin of the electron per orbital
For instance, let's take a look at carbon's electron configuration:
#C: [He]2s^(2)2p^2#
It would contain 2 core electrons, 4 valence electrons, 2 unpaired electrons and three orbitals:
#n#: #1, 2#
#l#: #0,1#
#m_l#: #[-1,1]#
#m_s#: #1/2,-1/2# the only two it may possess, ever
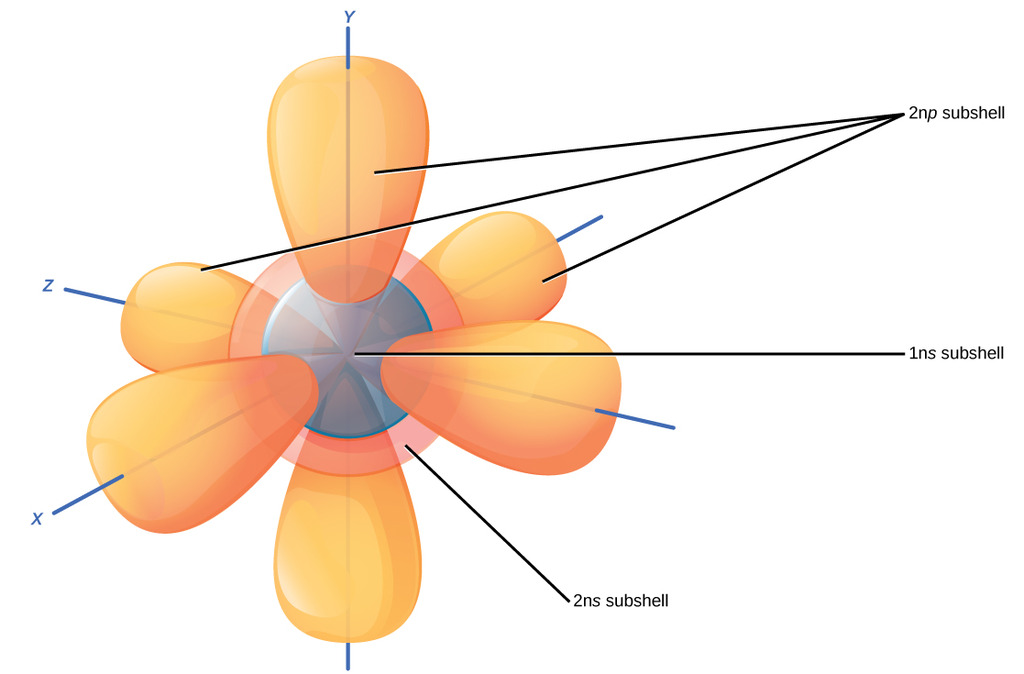
In more detail, the #1s,# and #2s# orbitals are full of two electrons each, each a sphere in increasing size proportional to #n#. The #2p# orbital has two unpaired electrons in accordance with Hund's rule, and three spatial orientations. It'd look something like this