How do you write # y=|x+1|-4# as a piecewise function?

Question

6938 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-16T05:40:13

#color(blue)(|x+1| - 4 = { x+1, if x>= (-1)})#

#color(blue)(|x+1| - 4 = { -x-1, if x< (-1)})#

Given:

#color(red)(y=f(x)=|x+1|-4)#

We draw the graph of this function first

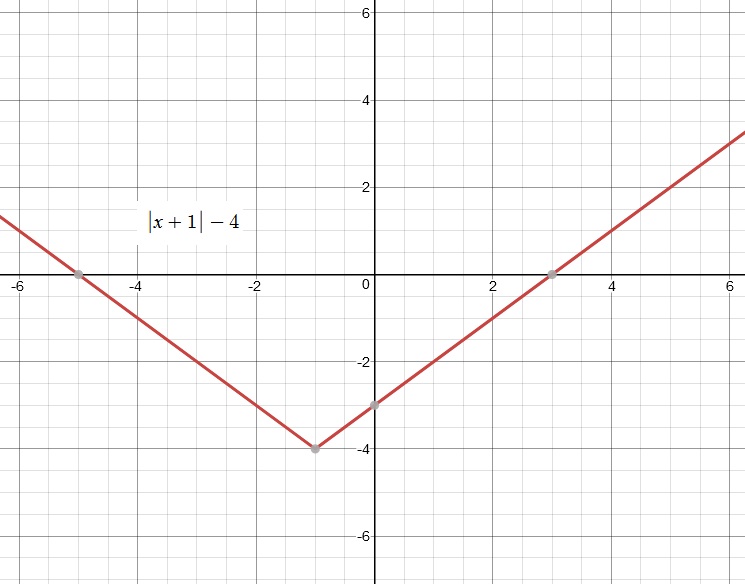
enter image source here

#color(green)(Step.1)#

We find the boundary line first.

Later, once we find the "Piece-wise Functions", we can graph those as well and compare the graphs.

We can accomplish this process by setting what is inside absolute value to ZERO, and then solving for #color(red)x#.

So, when

#x+1 =0#

we get

#color(blue)(x = (-1))#

#color(green)(Step.2)#

When #(x+1)# is Positive, we just consider the expression as it is,

but if #(x+1)# is Negative, we must negate the whole expression

#color(green)(Step.3)#

Hence,

our required Piece-wise Functions are

#color(blue)(|x+1| - 4 = { x+1, if x>= (-1)})#

#color(blue)(|x+1| - 4 = { -x-1, if x< (-1)})#

We will graph the Piece-wise Functions below:

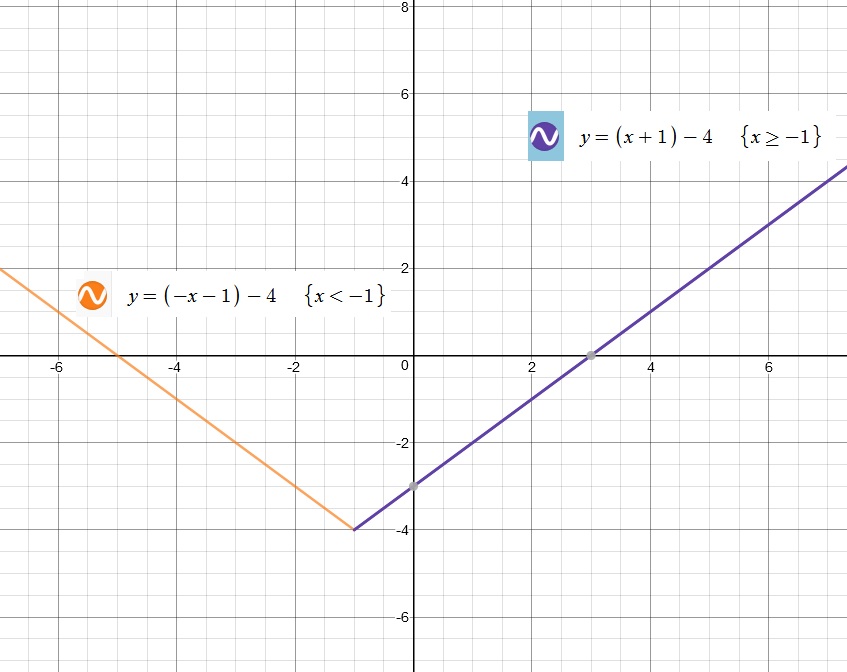
enter image source here

Hope this helps.