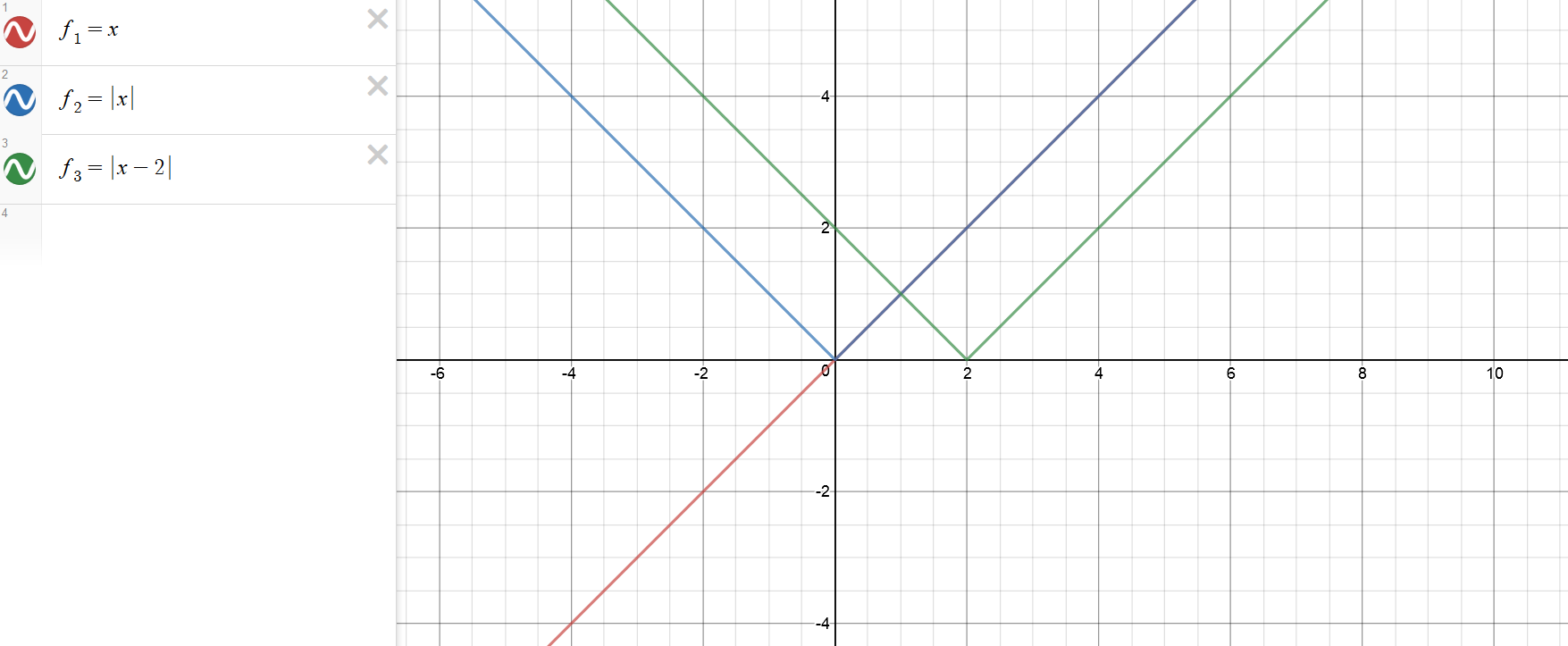
How do you write #y = | x - 2|# as piecewise functions?
2 Answers
See a solution process below:
Explanation:
Step 1) First, solve the term within the absolute value function for
Step 2) Multiply the term within the absolute value function by
Step 3) Take the term within the absolute value function and write a "greater than or equal to" inequality with the result of Step 1:
Step 4) Combine Step 2 & Step 3 to form the piecewise function:
see below
Explanation:
Absolute value mirrors every negative value to the positive according to x axis.
And finally, a number inside absolute value moves graph to the right or left. When it's minus: