Question

How does rate of change relate to slope?

Answer 1

As below.

Explanation:

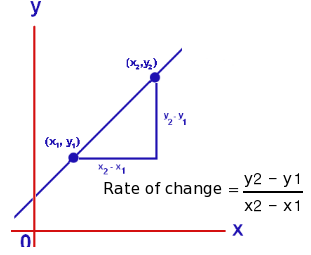
Slope is the ratio of the vertical and horizontal changes between two points on a surface or a line.
The vertical change between two points is called the rise, and the horizontal change is called the run.
The slope equals the rise divided by the run: .
This simple equation is called the slope formula.

If `y = f(x+h) = 3 (x + h)^ 2`, (Just plug x + h in for x). So, you get this:

The instantaneous rate of change, or derivative, can be written as dy/dx, and it is a function that tells you the instantaneous rate of change at any point.

`y' = f'(x+h) = (d/(dx)) (3*(x)^2) = 6x * 1 = 6x`

. For example, if x = 1, then the instantaneous rate of change is 6.

Rate of Change Formula helps us to calculate the slope of a line if the coordinates of the points on the line are given. ... If coordinates of any two points of a line are given, then the rate of change is the ratio of the change in the y-coordinates to the change in the x-coordinates.

Hope this helps.