Rates of Change
Key Questions
-
Answer:
As below.
Explanation:
Slope is the ratio of the vertical and horizontal changes between two points on a surface or a line.
The vertical change between two points is called the rise, and the horizontal change is called the run.
The slope equals the rise divided by the run: .
This simple equation is called the slope formula.
If
#y = f(x+h) = 3 (x + h)^ 2# , (Just plug x + h in for x). So, you get this:
The instantaneous rate of change, or derivative, can be written as dy/dx, and it is a function that tells you the instantaneous rate of change at any point.
#y' = f'(x+h) = (d/(dx)) (3*(x)^2) = 6x * 1 = 6x# . For example, if x = 1, then the instantaneous rate of change is 6.
Rate of Change Formula helps us to calculate the slope of a line if the coordinates of the points on the line are given. ... If coordinates of any two points of a line are given, then the rate of change is the ratio of the change in the y-coordinates to the change in the x-coordinates.
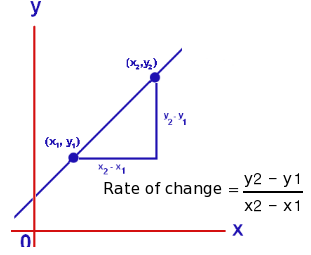
Hope this helps.
-
Rate of change is a number that tells you how a quantity changes in relation to another.
Velocity is one of such things. It tells you how distance changes with time.
For example: 23 km/h tells you that you move of 23 km each hour.Another example is the rate of change in a linear function.
Consider the linear function:
#y=4x+7#
the number 4 in front of#x# is the number that represent the rate of change. It tells you that every time#x# increases of 1, the corresponding value of#y# increases of 4.
If you get a negative number it means that the#y# value is decreasing.
If the number is zero it means that you do not have change, i.e you have a constant!Examples:
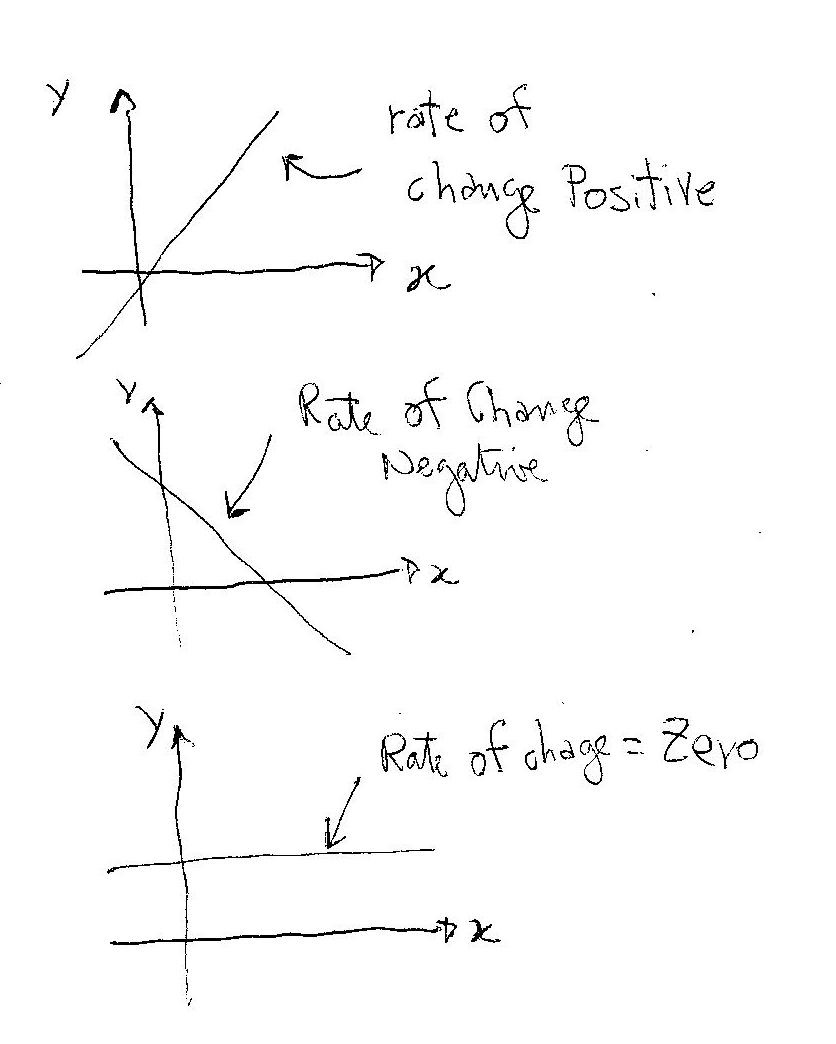
-
Average Rate of Change
The average rate of change of a function
#f(x)# on an interval#[a,b]# can be found by#("Average Rate of Change")={f(b)-f(a)}/{b-a}#
Example
Find the average rate of change of
#f(x)=x^2+3x# on#[1,3]# .#f(3)=(3)^2+3(3)=18# #f(1)=(1)^2+3(1)=4# #("Average Rate of Change")={f(3)-f(1)}/{3-1}={18-4}/{2}=14/2=7#
I hope that this was helpful.
Questions
Graphs of Linear Equations and Functions
-
Graphs in the Coordinate Plane
-
Graphs of Linear Equations
-
Horizontal and Vertical Line Graphs
-
Applications of Linear Graphs
-
Intercepts by Substitution
-
Intercepts and the Cover-Up Method
-
Slope
-
Rates of Change
-
Slope-Intercept Form
-
Graphs Using Slope-Intercept Form
-
Direct Variation
-
Applications Using Direct Variation
-
Function Notation and Linear Functions
-
Graphs of Linear Functions
-
Problem Solving with Linear Graphs