How does the graph of #f(x) = log_2(x - 5) - 2# compare to its parent function f(x) = #log_2 x#?
1 Answer
Sep 7, 2015
Explanation:
For any function
From this we can quickly see that
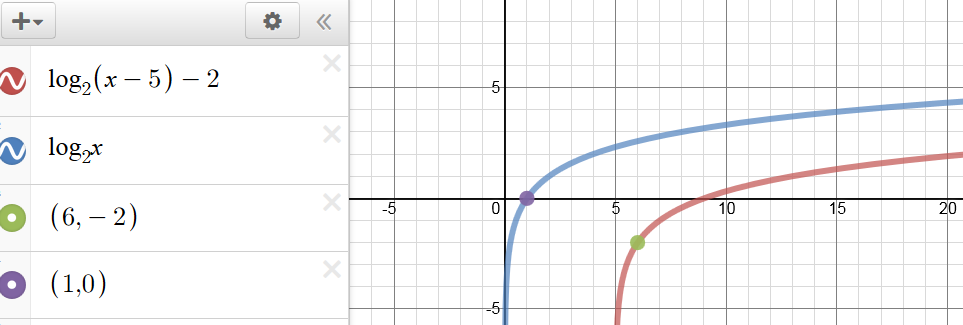
For any function
From this we can quickly see that
