Question

How does the graph of `y=sqrt(x+3) -4` compare with `y=sqrtx`?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`

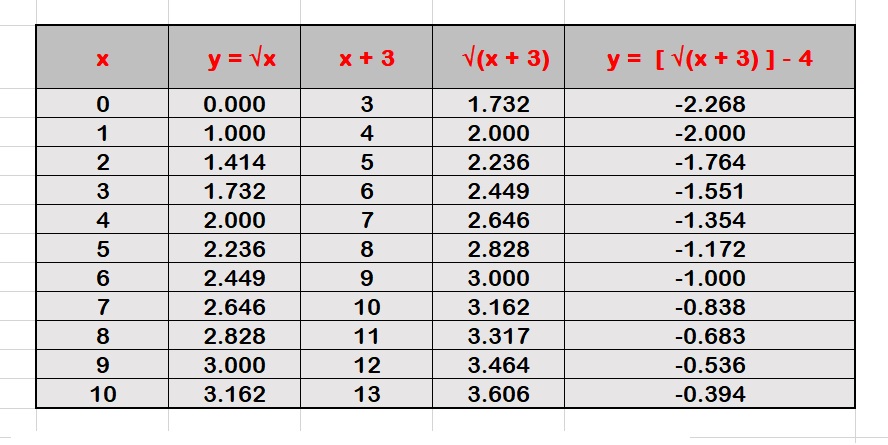
Use the following data table to generate the graph:

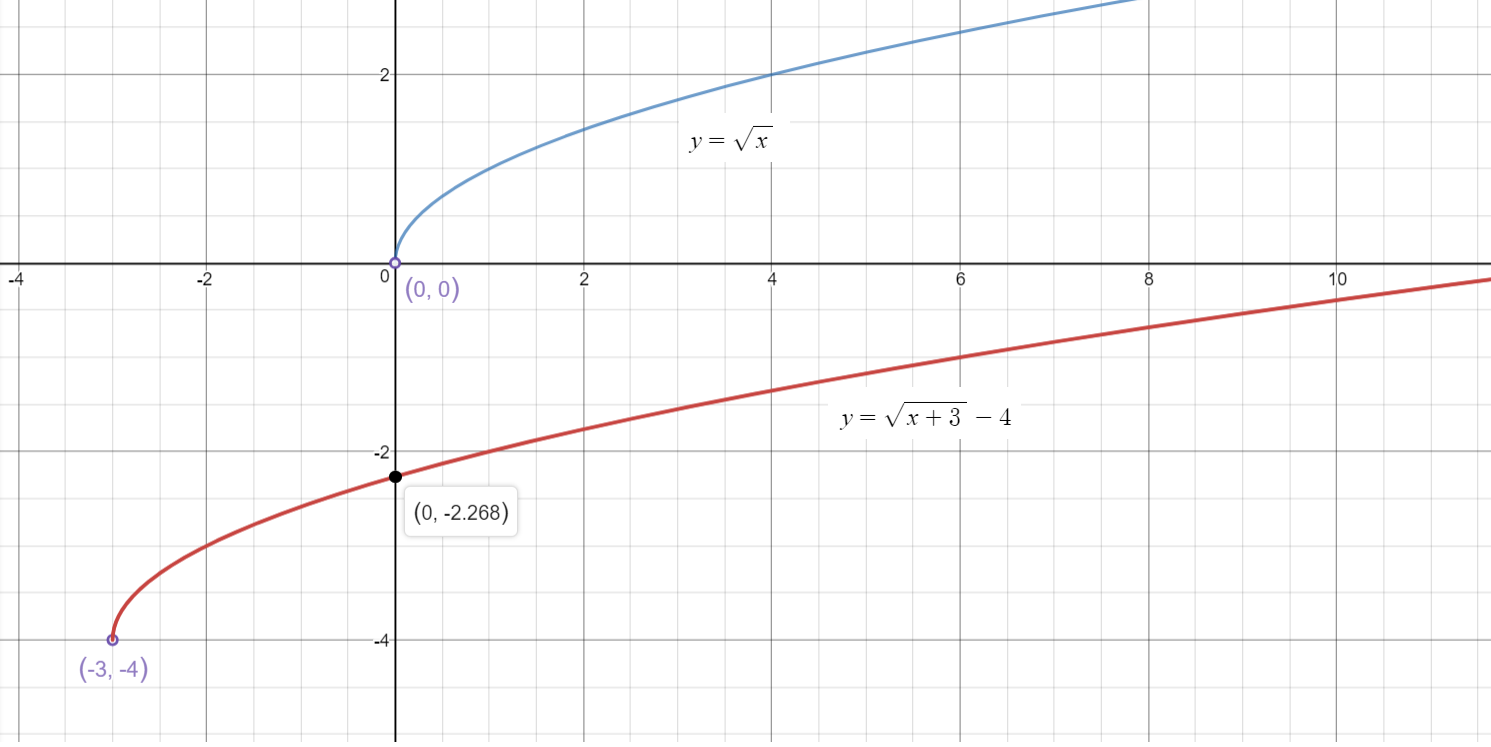
Observe the graphs given below:

1. Graph of `color(blue)(y=sqrt(x)`

2. Graph of `color(red)(y=sqrt(x+3)-4`

The radical function: `color(blue)(y=sqrt(x)` is the Parent Function:

The graph of the parent function starts at the origin `(0,0)`

The graph increases gradually.

The general form of the radical function:

`color(red)(y= f(x)=a sqrt[b(x-c)] +d`, where

( i). `color(red)(|a|` will stretch or shrink the graph vertically

( ii), `color(red)(|b|` will stretch or shrink the graph horizontally

(iii). `color(red)(c` will shift the graph left or right.

( iv). `color(red)(d` will shift the graph up or down.

( v). `color(red)(-a` will flip the graph across -axis

( vi). `color(red)(-b` will flip the graph across y-axis

For our problem, `color(blue)(a=1; b=1; c=-3; d=-4`

Since `color(red)(c` is negative, the graph is shifted to the left.

Since `color(red)(d` is negative, the graph is shifted down.

We can compare both the graphs (parent function and the function given) to comprehend the behavior of the parent graph and the graph of the corresponding radical function.

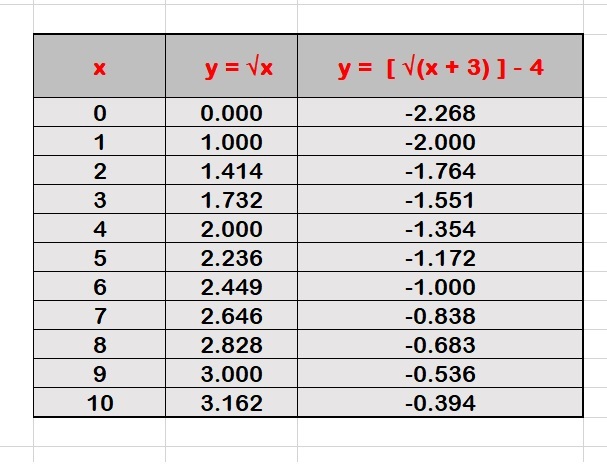
Data Table for the graph:

Graph:

Hope it helps.