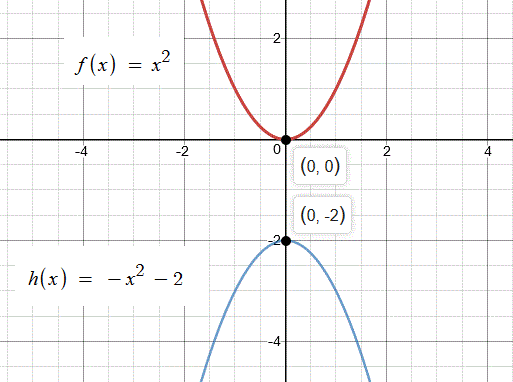Question

How is the graph of `h(x)=-x^2-2` related to the graph of `f(x)=x^2`?

Answer 1

We are given

`y = f(x) = x^2 and` ... Equation.1

`y = h(x) = -x^2-2 and` ... Equation.2

We need to explain how these graphs are related.

Please read the explanation.

Explanation:

Graph of the Parabola for the Quadratic Equation..

`color(red)(y = f(x)= x^2)` ... Equation.1

..opens up as the coefficient of `color(red)(x^2)` term is greater than ZERO.

Vertex is at `(0,0)`

We have a minimum value for this parabola.

The Vertex is on the Line of Symmetry of the parabola.

Line of Symmetry at x = 0 is the imaginary line where we could fold the image of the parabola and both halves match exactly.

In our problem, this is also the y-axis

Graph `color(red)(y = x^2)` is available below:

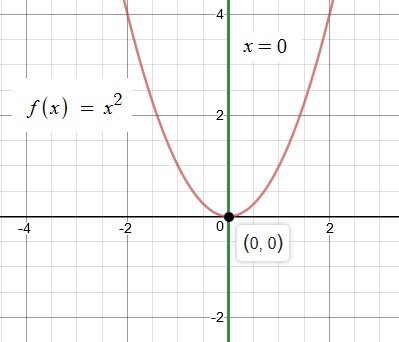
Next, we will consider the equation `color(red)(y=f(x)=-x^2`

For this equation the parabola opens down as the coefficient of `color(red)(x^2)` term is less than ZERO.

Vertex is at `(0,0)`

Line of Symmetry at x = 0

We have a maximum value for this parabola.

This parabola is a reflection of the graph of `color(red)(y = x^2`

Graph `color(red)(y = -x^2)` is available below:

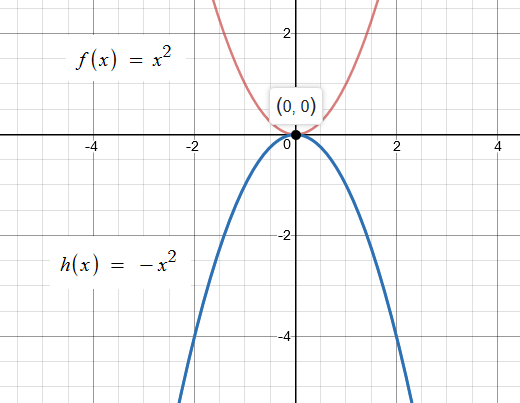
Next we will consider the equation

`color(red)(y = h(x) = -x^2-2 and` ... Equation.2

Vertex is at `(0,-2)`

Line of Symmetry at x = 0

This parabola is a shift of the graph of `color(red)(y = x^2` by `2` units down.

Graph `color(red)(y f(x) = = -x^2 - 2)` is available below: