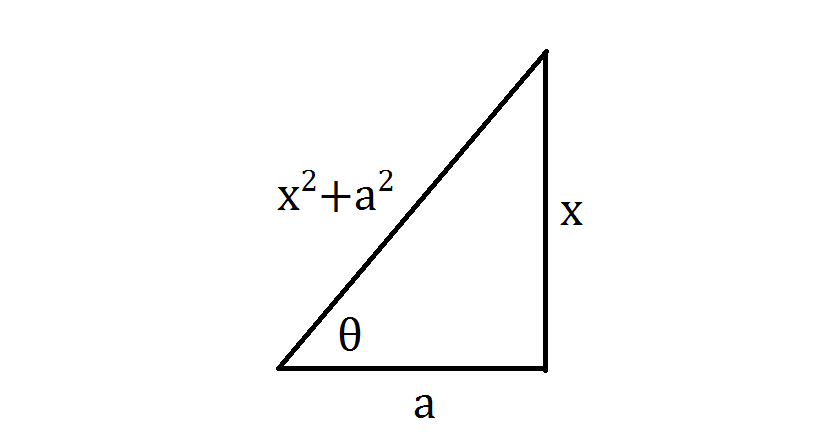I find both types of substitutions very fascinating because of the reasoning behind them. Consider, first, trig substitution. This stems from the Pythagorean Theorem and the Pythagorean Identities, probably the two most important concepts in trigonometry. We use this when we have something like:
#x^2+a^2-># where #a# is constant
#sqrt(x^2+a^2)-># again assuming #a# is constant
We can see that these two look awfully like #a^2+b^2=c^2#, which is the Pythagorean Theorem. It relates the two sides of a right triangle to the triangle's hypotenuse. If we draw this out, we can see that yes, #x^2+a^2# can be represented with a triangle:
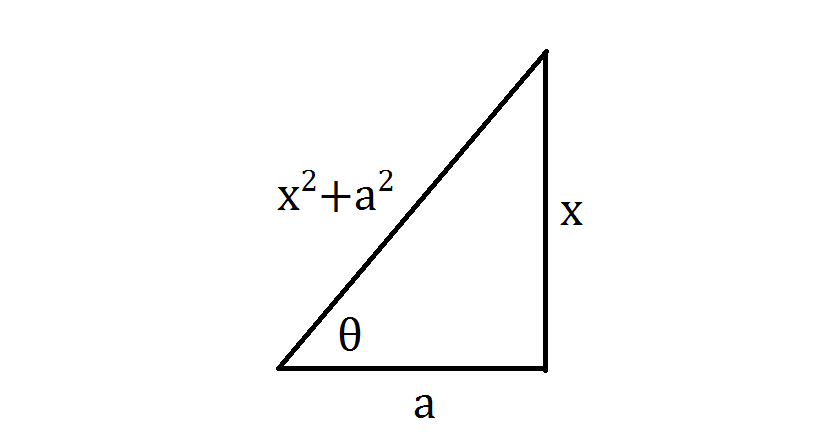
The picture is very useful, because it tells us #tantheta=x/a#, or #atantheta=x#; this forms the basis of the trig substitution. Furthermore (and this is where it gets awesome), when you substitute #x=tantheta# into #x^2+a^2#, you end up with a Pythagorean Identity, in this case #tan^2theta+1=sec^2theta#. You can then do some simplifying for #sec^2theta# if you need to, and the integral is easy there on out. The same goes for the cases #x^2-a^2#, #a^2-x^2#, #sqrt(x^2-a^2)#, and #sqrt(a^2-x^2)#.
You can use trig sub. for a good deal of problems, but you can use #u#-substitution arguably even more. We use this technique when we have something like #intlnx/xdx#. If we are observant, we see that we have two functions - #lnx# and #1/x#. And if we remember our basic derivatives, we know #d/dxlnx=1/x# for #x>0# (or #d/dxlnabs(x)=1/x# for #x!=0#). So the idea is to say let #u=lnx#; then #(du)/dx=1/x# and #du=dx/x#. The problem, after making these substitutions, simplifies to #intudu# - a much easier integral than before.
While these two techniques may be different, they both serve the same purpose: to reduce an integral to a simpler form so we can use basic techniques. I'm sure my explanation does not suffice to include all the specific details about these substitutions, so I invite others to contribute.