How many electrons in an atom can have the n = 5, l = 2 designation?

1 Answer
Stefan V.
Dec 24, 2016

#"10 electrons"#

Explanation:

All you really need in order to answer this question is a version of the Periodic Table of Elements that shows the blocks

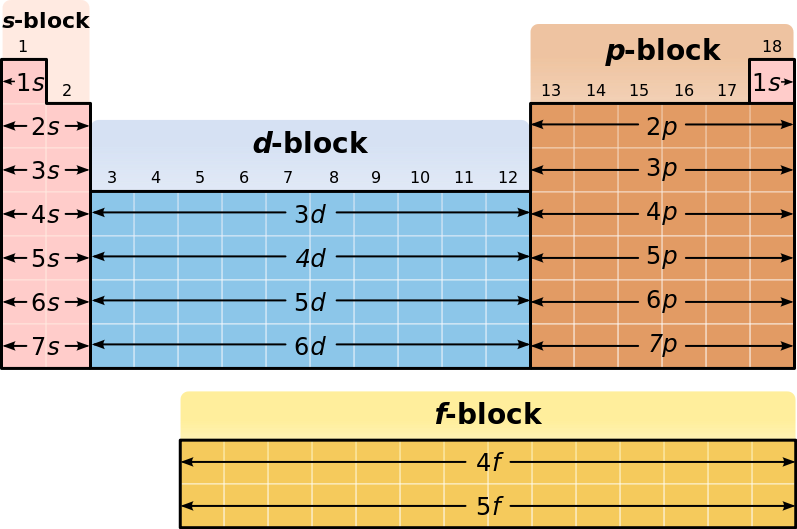
http://allfactsperiodictable.blogspot.ro/

Now, the principal quantum number, #n#, gives you the energy level on which the electron is located. This is equivalent to the period in which the element is located in the Periodic Table.

In your case, #n=5# designates an element located in period #5#.

Next, the angular momentum quantum number, #l#, tells you the subshell in which the electron resides. The subshells are equivalent to the blocks of the Periodic Table.

You have

  • #l=0 -># the s subshell #=# the s block
  • #l=1 -># the p subshell #=# the p block
  • #l=2 -># the d subshell #=# the d block
  • #l=3 -># the f subshell #=# the f block

In your case, #l=2# designates an electron located in the #d# block of the Periodic Table.

Now, the #d# block contains a total fo #10# groups, i.e. #10# columns of the Periodic Table. Each group is equivalent to #1# electron. This means that the #d# block, which is equivalent to the #d# subshell, can hold a total of #10# electrons.

Therefore, a maximum of #10# electrons can share the two quantum numbers

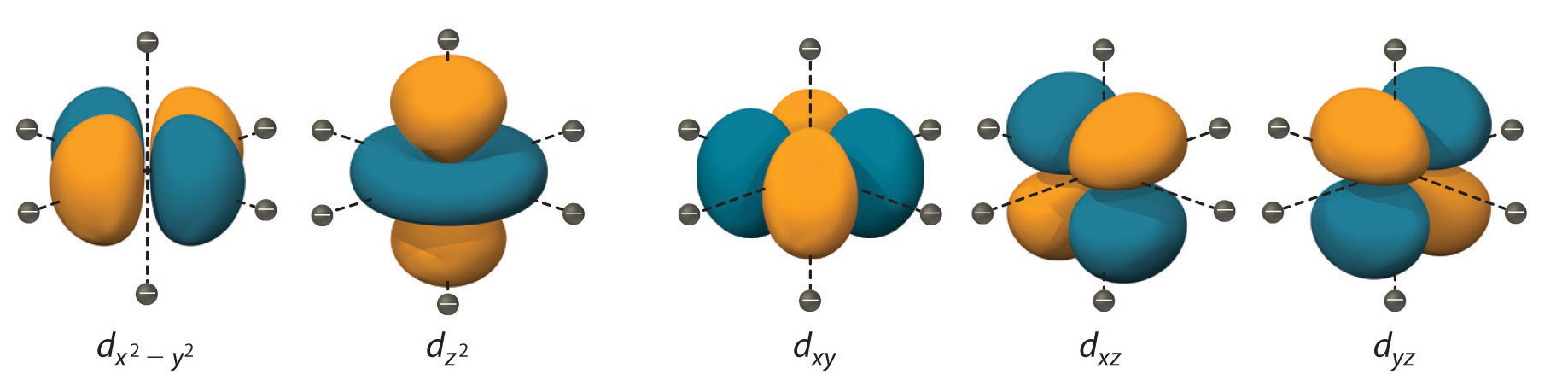
#n=5, l=2#

These electrons are located on the fifth energy level, in the d subshell, i.e. in one of the #5# d orbitals shown below

http://chemistryjee.blogspot.ro/2015/08/crystal-field-theory.html

As a side note, you can find the number of orbitals that can exist in a subshell by dividing the number of groups in a block by #2#

#"no. of orbitals in a subshell" = "no. of groups in the block"/2#

This is the case because an orbital can hold a maximum of #2# electrons as stated by the Pauli Exclusion Principle.

Related questions
See all questions in Quantum Numbers
Impact of this question
130953 views around the world
You can reuse this answer
Creative Commons License