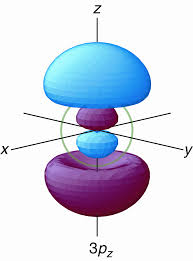
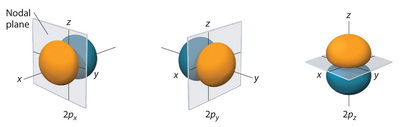
How many nodal points 3p orbital have?
1 Answer
Jul 6, 2017
Not sure what you mean by points, but the
- a principal quantum number
#n = 3# , placing it on the third energy level. - an angular momentum quantum number
#l = 1# , giving it the shape of a#p# orbital.
The number of radial nodes, otherwise known as spherical shell nodes, is given by
#n - l - 1 = 3 - 1 - 1 = bb1# radial nodein the
#3p# orbital (see the green circle in the image above).
The number of angular nodes (or nodal planes, for orbitals that are not the
#l = bb1# angular node (here, nodal plane)in the
#3p# orbital (the plane perpendicular to the orbital axis).
Thus, the total number of nodes (regardless of type) is given by
#n - 1 = 3 - 1 = bb2# total nodes in general in the#3p# orbital.
Nodal planes are depicted more explicitly here: