s,p,d,f Orbitals
Key Questions
-
Answer:
#2, 6, 10, 14# respectivelyExplanation:
If
#ℓ# is the angular quantum number of subshell then maximum electrons it can hold is#2(2 ℓ + 1)# #underline(bb("Sub-shell" color(white)(.....) ℓ color(white)(.....) "Maximum electrons"))#
#color(white)(.....)"s" color(white)(..............) 0 color(white)(............) 2(2(0) + 1) = 2#
#color(white)(.....)"p" color(white)(...............) 1 color(white)(............) 2(2(1) + 1) = 6#
#color(white)(.....)"d" color(white)(...............) 2 color(white)(............) 2(2(2) + 1) = 10#
#color(white)(.....)"f" color(white)(....._........) 3 color(white)(............) 2(2(3) + 1) = 14# -
Answer:
Orbitals are the regions of space in which electrons are most likely to be found.
Explanation:
Each orbital is denoted by a number and a letter.
The number denotes the energy level of the electron in the orbital. Thus 1 refers to the energy level closest to the nucleus; 2 refers to the next energy level further out, and so on.
The letter refers to the shape of the orbital. The letters go in the order s, p, d, f, g, h, i, j, etc. The letters s, p, d, and f were assigned for historical reasons that need not concern us. All we have to do is remember the shapes that correspond to each letter.
Since an electron can theoretically occupy all space, it is impossible to draw an orbital. All we can do is draw a shape that will include the electron most of the time, say 95% of the time. We call this shape the 95% contour.
s ORBITALS
An s orbital is spherically symmetric around the nucleus of the atom, like a hollow ball made of rather fluffy material with the nucleus at its centre. As the energy levels increase, the electrons are located further from the nucleus, so the orbitals get bigger. The order of size is 1s < 2s < 3s < …, as shown below.
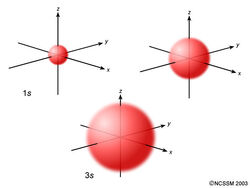
Now, let’s look at a cross-section of these orbitals.

If you look carefully, you will notice that a 1s orbital has very little electron density near the nucleus, but it builds up to a maximum as you get further from the nucleus and then decreases beyond the contour. It is sort of like a hollow tennis ball.
A 2s orbital is similar to a 1s orbital, but it has sphere of electron density inside the outer sphere, like one tennis ball inside another. There is a surface between the two balls where there is zero probability of finding an electron. We call this surface a node or a nodal surface.
A 3s orbital is even larger, and it has three nodes.
p ORBITALS
Not all electrons inhabit s orbitals. At the first energy level, the only orbital available to electrons is the 1s orbital. However, at the second level, there are also orbitals called 2p orbitals in addition to the 2s orbital.
Unlike an s orbital, a p orbital points in a particular direction. The one shown below points up and down the page.

At any one energy level, we have three absolutely equivalent p orbitals pointing mutually at right angles to each other. These are arbitrarily given the symbols px, py and pz. This is simply for convenience, because what you might think of as the x, y or z direction changes constantly as the atom tumbles in space.
The p orbitals at the second energy level are called 2px, 2py and 2pz. There are similar orbitals at subsequent levels: 3px, 3py, 3pz, 4px, 4py, 4pz and so on.
All levels except the first have p orbitals.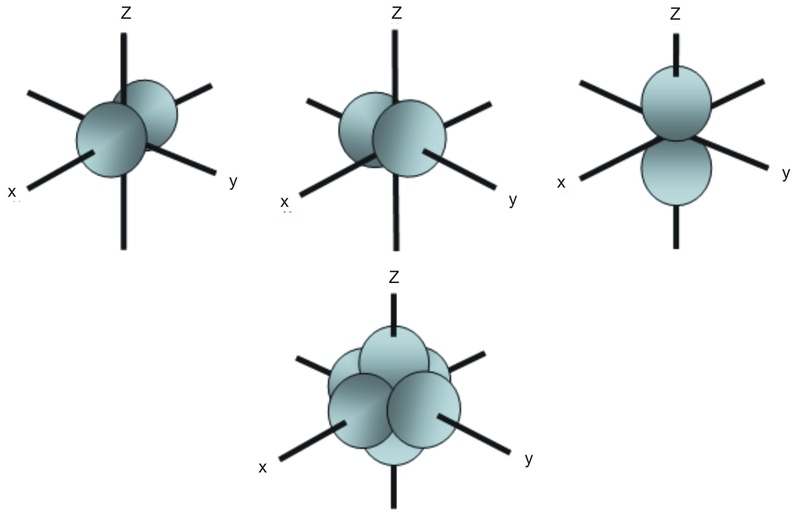
d ORBITALS
In addition to s and p orbitals, there are two other sets of orbitals which become available for electrons to inhabit at higher energy levels. At the third level, there is a set of five d orbitals (with complicated shapes and names) as well as the 3s and 3p orbitals (3px, 3py, 3pz). At the third level there are a total of nine orbitals altogether.
The five 3d orbitals are called
3dxy
3dxz
3dyz
3dx² - y²
3dz²
To make sense of the names, we need to look at them in two groups. The first group contains the 3dxy, 3dxz and 3dyz orbitals. The names tell you that these orbitals lie in the x-y plane, the x-z plane, and the y-z plane, respectively. Each orbital has four lobes, and each of the lobes is pointing between two of the axes, not along them.
The second group contains the 3dx² - y² and 3dz² orbitals. Their lobes point along the various axes.
The 3dx² - y² orbital looks exactly like the first group, except that that the lobes are pointing along the x and y axes, not between them.
The 3dz² looks like a p orbital wearing a doughnut around its waist.
f ORBITALS
At the fourth and higher levels, there are seven f orbitals in addition to the 4s, 4p, and 4d orbitals.
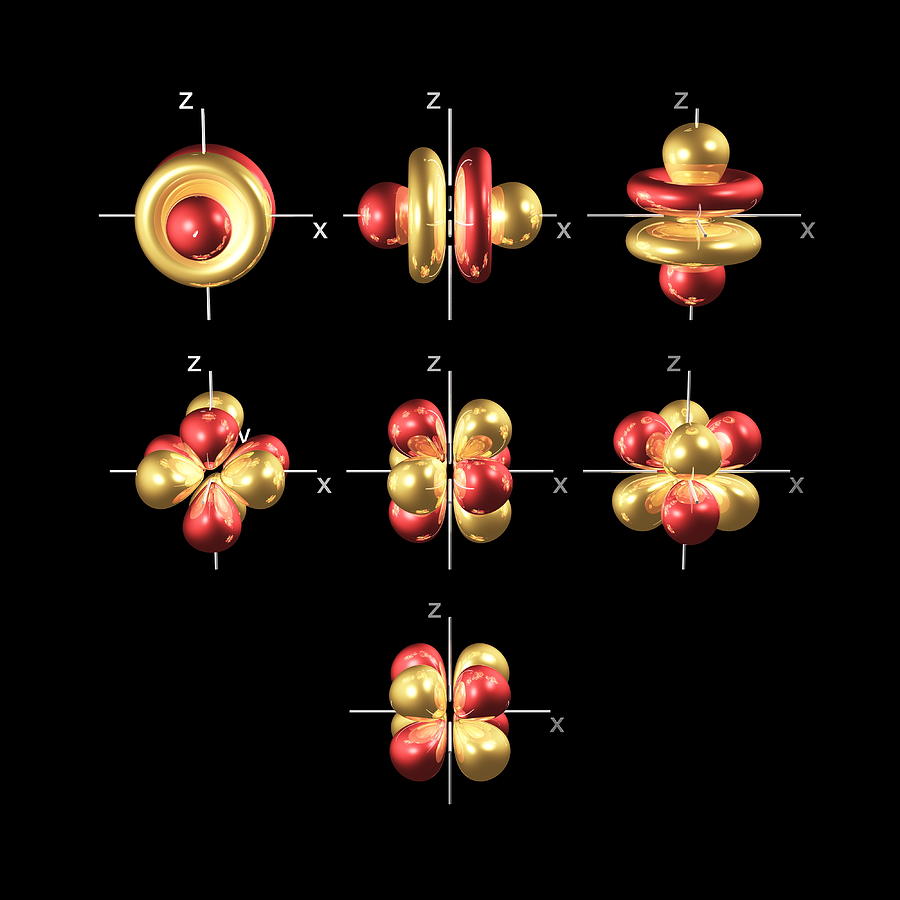
Counting the 4s, 4p, and 4d orbitals, this makes a total of 16 orbitals in the fourth level. They have even more complicated shapes. s, p, d, and f orbitals are available at all higher energy levels as well. Fortunately, you will probably not have to memorize the shapes of the f orbitals. Just remember that there seven f orbitals in each level from level 4 and onwards.