How much work does it take to push an object with a mass of #4 kg # up a #9 m # ramp, if the ramp has an incline of #(5pi)/12 # and a kinetic friction coefficient of # 8 #?
1 Answer
The work done by the push is
Explanation:
I will show show how to find the work done by the push. There are two methods to doing this, so I'll show both. This will be a lengthly explanation.
An important tool in solving this problem is the work-energy theorem, which states that the work done is equal to the change in energy of a system:
#W=DeltaE_(system)#
The total work done by nonconservative forces is equal to the change in mechanical energy of a system, and is given by:
#W_(nc)=DeltaE_(mech)# A nonconservative force is a force for which work is not path independent, as opposed to a conservative force, where the work done on an object as it moves from an initial to final position is independent of the path followed. This makes it possible to define a potential at any given point. It is not possible to define a potential energy for a nonconservative force. Examples of conservative forces include gravity, magnetism, and force in an elastic spring. Examples of nonconservative forces include friction and air resistance.
The second method involves the work-energy theorem for kinetic energy, given by:
#W_(n e t)=DeltaK# Where
#DeltaK# is the change in kinetic energy.
Work done by a constant force is given by:
#W=vecFDeltarcos(theta)# Where
#vecF# is the applied force,#Deltar# is the displacement, and#theta# is the angle between the force and displacement vectors.Note that work is done by forces which act parallel to the displacement; forces which act perpendicular to displacement do no work (
#theta=90^o,270^o# ;#cos(90^o), cos(270^o)=0# )
A force diagram for pushing the object up the ramp:
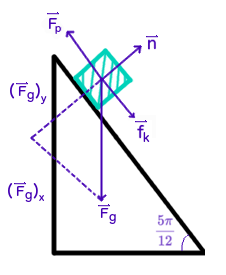
Where
#vecF_p# is the force of the push,#vecf_k# is the force of kinetic friction,#vecn# is the normal force,#vecF_g# is the force of gravity, and#vecF_(gx)# and#vecF_(gy)# are the parallel and perpendicular components of the force of gravity, respectively.Forces acting parallel to the motion (pushing the object up the ramp) are the force of the push, the force of kinetic friction, and the parallel component of gravity. The others act perpendicular to the motion (
#vecn, vecF_(gy)# ). As stated above, only parallel forces (relative to the motion) do work. We are only concerned with the nonconservative forces in this diagram for#W_(nc)# , which are the force of the push and the force of kinetic friction.
By the work-energy theorem:
#W_p+W_f=DeltaE_(mech)#
Using the equation for constant forces,
#W_p=vecF_p*Deltar*cos(theta)#
#W_f=vecf_k*Deltar*cos(theta)#
Method 1
To find the work done by the push, we solve the above work-energy equation for
#Wp=DeltaE_(mech)-W_f#
The change in mechanical energy is given by
#DeltaE=DeltaK+DeltaU# Where
#DeltaK# is the change in kinetic energy and#DeltaU# is the change in potential energy.
In pushing the object from the bottom of the ramp to the top, we begin and end at rest, so we aren't concerned with kinetic energy (i.e. there is no overall change in
#DeltaE=DeltaU#
#=>DeltaE=U_f-U_i#
The only potential energy we are concerned with is gravitational, given by
#DeltaE=mgh#
#=>Wp=mgh-W_f# Note that
#h# is the height of the ramp and can be found using basic trigonometry.
#sin(theta)=h/r=>h=rsin(theta)#
As stated above,
#vecf_k=mu_kvecn# Where
#mu_k# is the coefficient of kinetic friction and#vecn# is the normal force. We can calculate#vecf_k# to find the work done by friction.
Revisiting the force diagram above, we can produce parallel and perpendicular sum of forces statements:
#sumvecF_x=vecF_p-vecf_k-vecF_(gx)=mveca_x#
#sumvecF_y=vecn-vecF_(gy)=mveca_y#
As the object is not accelerating vertically:
#vecn-vecF_(gy)=0#
#=>vecn=vecF_(gy)#
We can find the perpendicular component of gravity using basic trigonometry, where
#cos(theta)=(vecF_(gy))/(vecF_g)#
#vecF_(gy)=vecF_gcos(theta)# Note that the angle between
#vecF_g# and#vecF_(gy)# is equal to the incline of the ramp (by geometry).
Therefore,
#f_k=mu_k*mgcos(theta)#
And work done by friction is:
#W_F=mu_kmgcos(theta)(Deltar)cos(theta)# The second
#cos(theta)# is the cosine of the angle between the force and displacement vectors. Because friction works opposite the motion, this is#theta=180^o# , which produces#cos(180^o)=-1# and gives us an overall negative work done by friction. This is expected given that friction works opposite the motion. This is how it is shown mathematically.
#W_F=-mu_kmgcos(theta)(Deltar)# .
We now have all the values necessary to calculate the work done by the push.
#W_p=mg(rsin(theta))-(-mu_kmgcos(theta)(Deltar))#
#=>W_p=mgrsin(theta)+mu_kmgcos(theta)(Deltar))#
#=>W_p=(4kg)(9.8m/s^2)(9m)sin((5pi)/12)+ (8)(4kg)(9.8m/s^2)cos((5pi)/12)(9m)#
#=>W_p=1071J# or
#W_p~~1xx10^3J#
Method 2:
We can also use the work-energy theorem for kinetic energy to solve.
#W_(n e t)=DeltaK#
As we have no net change in kinetic energy (object begins and ends at rest):
#=>W_(n e t)=0#
The net work is that done by each of the forces which act perpendicular to the motion, both conservative and nonconservative.
#=>W_(n e t)=W_p-W_(gx)-W_f=0#
Solve for
#W_p=W_f+W_(gx)#
#W_p=mu_kmgcos(theta)(Deltar)+mgsin(theta)(Deltar)#
#W_p=(8)(4kg)(9.8m/s^2)cos((5pi)/12)(9m)+(4kg)(9.8m/s^2)sin((5pi)/12)(9m)#
#W_p=1071J#
Hope that helps!

