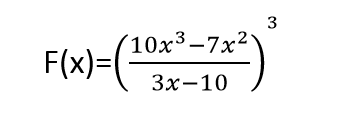As #F(x)=((10x^3-7x^2)/(3x-10))^3#, let #G(x)=(10x^3-7x^2)/(3x-10)#
then we can use chain rule as #F(x)=[G(x)]^3#.
But before that let us workout #(dG)/(dx)#
using Quotient rule, which states if #f(x)=(u(x))/(v(x))#
then #(df)/(dx)=((du)/(dx)xxv(x)-(dv)/(dx)xxu(x))/(v(x))^2#
In #G(x)=(10x^3-7x^2)/(3x-10)#, we have #u(x)=10x^3-7x^2# and #v(x)=3x-10#.
and #(du)/(dx)=30x^2-14x# and #(dv)/(dx)=3#
Hence, #(dG)/(dx)=((30x^2-14x)xx(3x-10)-3xx(10x^3-7x^2))/(3x-10)^2#
= #((90x^3-300x^2-42x^2+140x)-(30x^3-21x^2))/(3x-10)^2#
= #(60x^3-321x^2+140x)/(3x-10)^2#
Now #(dF)/(dx)=3(G(x))^2xx(dG)/(dx)#
= #3((10x^3-7x^2)/(3x-10))^2xx(60x^3-321x^2+140x)/(3x-10)^2#
= #(3(10x^3-7x^2)^2(60x^3-321x^2+140x))/(3x-10)^4#