How to find the roots of polynomial equation #2x^3+2x^2-19x+20=0#?
1 Answer
Solution set is
Explanation:
NOTE: I WROTE THIS ANSWER THINKING THE QUESTION WAS TO SOLVE FOR
Step 1: List the possible factors of this equation
This will be done using the rational root theorem, which states that the factors of
Therefore, our possible factors are given by
Step 2: Check these factors using the remainder theorem
This is when the trial and error process comes into play. The remainder theorem is useful because you can check the remainders without actually having to do the division.
It states that if
Step 3: Use long division to simplify the equation
We have now found one root. We're not quite certain of the others yet. We can now simplify the equation to a quadratic by using long division or synthetic division.
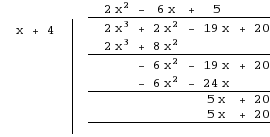
According, to the table above, the quotient is
#x = (-(-6) +- sqrt((-6)^2 - 4(2)(5)))/(2(2))#
#x = (6 +- sqrt(-4))/4#
#x = (6 +- 2sqrt(-1))/4#
We now use the identity
#x = (6 +- 2i)/4#
#x = (3 +- i)/2#
Hopefully this helps!

