Question

A monopolist faces a demand curve P = 70 - 1Q, with marginal revenue MR = 70 - 2Q, and MC = 20. Price is expressed in dollars.?

a)How to graph the three functions on one diagram.
b) How to compute the profit-maximizing output and price combination on the graph.
c) How to compute the efficient level of output (where MC = demand) on the graph
d) How to compute the deadweight loss associated with producing the profit-maximizing output rather than the efficient output ?

Answer 1

Profit maximising quantity and price combination.
Price `=$.45`
Quantity `=25 units`
DWL `=$312.5`

Explanation:

Given -

`p=70 - Q`------ -----------[Demand function]
`MR=70-2Q`---------------[Marginal Revenue function]
`MC=20`--------------------[Marginal Cost function]

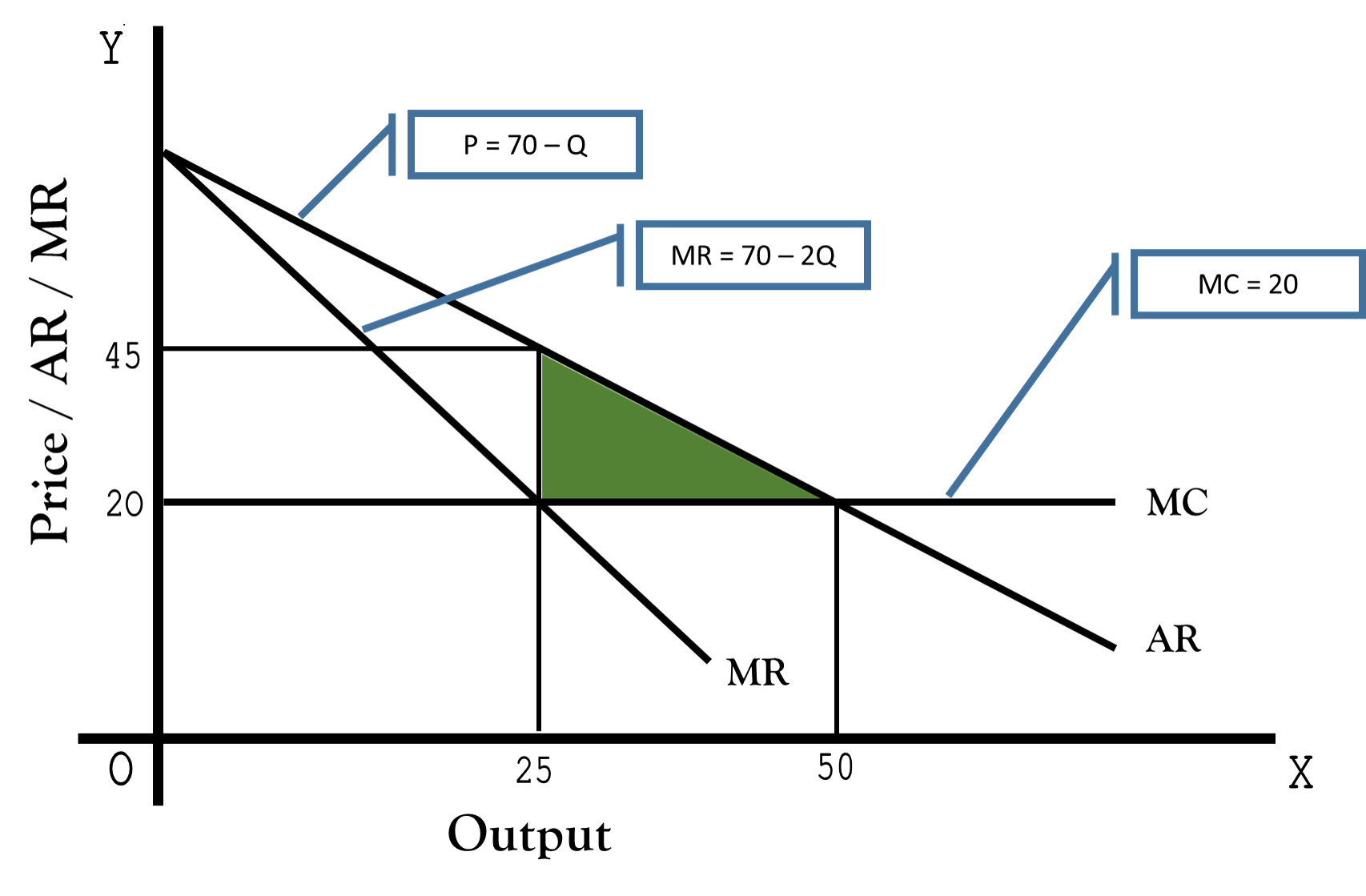
Profit Maximising Price and Output combination

Condition for maximum profit

`MR = MC`

`70-2Q=20`
`-2Q=20-70=-50`
`Q=(-50)/(-2)=25`
Profit maximising quantity `=25` units

Substitute `Q=25` in demand function to find the price

`p=70-Q`
`p=70-25=45`

Profit maximising price `=$45`

Condition for Efficient level of output

`D= MC`
`70-Q=20`
`-Q=20-70=50`
`Q=50`

Efficient level of output `=50` units

Dead Weight Loss is the green colour area.

DWL `=(25 xx 25)/2=312.5` ----- [Area of the green shaded area - height of the triangle is 25 and base of the triangle is 25]
DWL `=$312.5`