Question

How to graph a parabola `x=(y^2) - 4y + 3`?

Answer 1

You prepare a chart of `x` and `y` values and plot the points.

Explanation:

`x= y^2 -4y +3`

Note that `x` is the dependent variable and `y` is the independent variable.

Step 1. Prepare a chart.

Try an interval from `y = -5` to `y = 5`, and calculate the corresponding values of `x`.

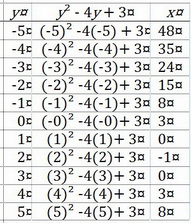
Step 2. Plot these points.

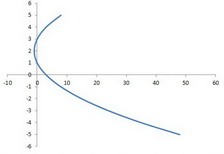
Step 3. Add points to make the plot symmetrical.

We need some extra points on the top portion of the graph.

Let's extend our table to `y = 10`.

Here's the extended portion of the table.

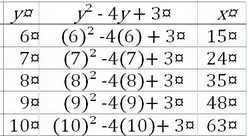
Add these extra points to the plot.

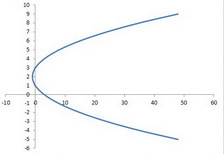
And we have our graph.

Answer 2

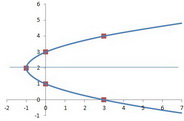
If the question is to sketch the parabola, you plot the vertex and the `x`- and `y`-intercepts, and draw a smooth line through them.

Explanation:

Warning! This is a long answer.

`x= y^2 -4y +3`

Note that `x` is the dependent variable and `y` is the independent variable.

We are going to get a sideways parabola.

Step 1. Define your variables.

The standard form for the equation of this parabola is

`x = ay^2 +by +c`

So

`a= 1`, `b = -4`, and `c = 3`

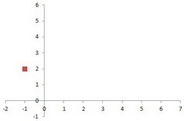
Step 2. Calculate and plot the vertex.

The vertex of the curve is given by

`y = -b/(2a) = -(-4)/(2×1) = -(-2) = 2`

Calculate the x-coordinate of the vertex.

`x= y^2 -4y +3 = (2)^2 -4(2) + 3 = 4 -8 + 3 = -1`

So the vertex is at (`-1,2`).

Plot your vertex point.

Step 3. Find the direction of the opening.

The parabola will be a sideways U opening either to the right (`⊂`) or to the left (`⊃`).

Since the coefficient `a` is positive, the parabola opens in the positive direction (to the right).

Step 4. (optional) Draw the parabola's axis of symmetry.

A parabola's axis of symmetry is a line that runs through its middle and divides it in half.

For a quadratic of the form `x = ay^2 +by +c`, the axis is a line that passes through the vertex and is parallel to the `y` axis.

For our parabola, the axis is the line #y = 2.

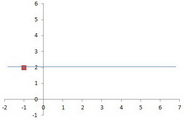
It's not part of the parabola itself, but lightly marking this line on your graph can help you see how the parabola curves symmetrically.

Step 5. Calculate and plot the `x`-intercept.

`x= y^2 -4y +3 = (0)^2 -4(0)+3 = 0 – 0 + 3 = 3`

The `x`-intercept is at (`3,0`). Plot this point.

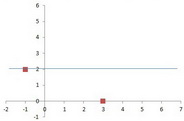
Step 6. Calculate and plot any `y`-intercepts.

`f(y) = y^2 -4y +3 = 0`
`(y-3)(y-1) = 0`
`y-3 = 0` or `y-1 = 0`
`y = 3` or `y = 1`

The x-intercepts are at (`0,3`) and (`0,1`).

Add these points to the graph.

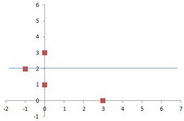
Step 7. Add any extra points to the graph.

The `x`-intercept at (`3,0`) is 2 units below the axis. There should be a corresponding point 2 units above the axis at (`3,4`).

Plot this point.

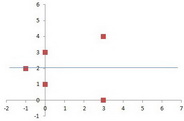
Step 7. Draw a smooth parabola passing through all the points.