Question

How to solve this? Find `m in RR` for which `X^3-3X+m=0` has a double root.

Answer 1

`m=+-2`

Explanation:

Given:

`x^3-3x+m = 0`

Here's one method:

Suppose the roots are `alpha`, `alpha` and `beta`.

Then:

`x^3-3x+m = (x-alpha)(x-alpha)(x-beta)`

`color(white)(x^3-3x+m) = x^3-(2alpha+beta)x^2+(alpha^2+2alphabeta)x-alpha^2beta`

Equating coefficients, we have:

`{ (2alpha+beta = 0), (alpha^2+2alphabeta = -3), (-alpha^2beta = m) :}`

From the first equation, we have:

`beta = -2alpha`

Substituting this into the second and third equations, we find:

`{ (-3alpha^2 = -3), (2alpha^3 = m) :}`

From the first of these equations we find:

`alpha^2 = 1`

and hence:

`alpha = +-1`

Then from the second:

`m = 2alpha^3 = +-2`

Answer 2

`m in {-2,+2}`

Explanation:

There are a couple ways to approach this once we recognize that "having a double root" is equivalent to having a slope of zero.

Graphically, if we consider the simpler relation: `y=x^3-3x`

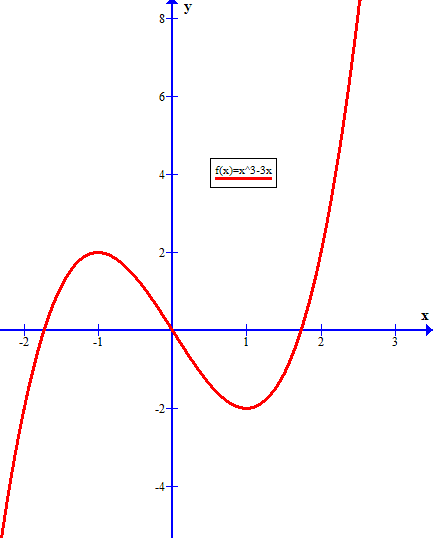
we can see that the relation has turning points at `(-1,2)` and `(1,-2)`
That is the relation has a double root when
`color(white)("XXX")2=x^3-3xcolor(white)("XX")rarrcolor(white)("XX")x^3-3xcolor(magenta)(-2)=0color(white)("XX")rarrcolor(white)("XX")m=color(magenta)(-2)`
and when
`color(white)("XXX")-2=x^3-3xcolor(white)("XX")rarrcolor(white)("XX")x^3-3xcolor(magenta)(+2)=0color(white)("XX")rarrcolor(white)("XX")m=color(magenta)(+2)`

Using Calculus
A slope of zero implies that the derivative is equal to zero at that point.
If `f(x)=x^3-3x+m` for some constant `m`
then the slope is zero when
`color(white)("XXX")(df)/(dx)=3x^2-3=0`
`color(white)("XXXXXXX")x^2=1color(white)("XX")rarrcolor(white)("XX")x=+-1`

Substituting `x=1` and `x=-1` back into the equation:
`color(white)("XXX")x^3-3x+m=0`
gives the solution values for `m`
`color(white)("XXX")m=2color(white)("X")andcolor(white)("X")m=-2`

Answer 3

`m = +-2`

Explanation:

Here's another method using the discriminant...

The discriminant `Delta` of a cubic `ax^3+bx^2+cx+d` is given by the formula:

`Delta = b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd`

The cubic will have repeated roots if and only if `Delta = 0`.

`x^3-3x+m = 0`

is in the form:

`ax^3+bx^2+cx+d = 0`

with `a=1`, `b=0`, `c=-3` and `d=m`

So:

`Delta = b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd`

`color(white)(Delta) = color(red)(cancel(color(black)((0)^2(-3)^2)))-4(1)(-3)^3-color(red)(cancel(color(black)(4(0)^3(m))))-27(1)^2(m)^2+color(red)(cancel(color(black)(18(1)(0)(-3)(m))))`

`color(white)(Delta) = 4*27 - 27m^2`

`color(white)(Delta) = 27(2^2-m^2)`

`color(white)(Delta) = 27(2-m)(2+m)`

So `Delta = 0` if and only if `m = +-2`

Answer 4

`m=+-2`

Explanation:

Another method

if a cubic has a repeated root `" "alpha" "`then we have:

`P(x)=(x-alpha)^2(x-beta)`

differentiating

`=>P'(x)=2(x-alpha)(x-beta)+(x-alpha)^2`

`:.P'(alpha)=2(alpha-alpha)(alpha-beta)+(alpha-alpha)^2=0`

ie for a repeated root `" "alpha" "`in a cubic `" "P'(alpha)=0`

so we have

`P(X)=X^3-3X-m`

`P'(X)=3X^2-3`

solving`" "3X^2-3=0=>X=+-1`

`X=1=>1^3-3xx1-m=0`

`=>m=-2`

`X=-1=>(-1)^3-3xx(-1)-m=0`

`=>m=2`