How do you write matrices on Socratic?
3 Answers
Hello!
I'll show you first how to write matrices without the programmed version, so you know what to type between the #.
Let's say we want to make this generic matrix:
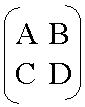
You would type ((a,b),(c,d))
So you put each row in a set of parenthesis and seperate your values from left to right with commas.. When you want to start a new row, you close the parenthesis, add a comma, and start a new set of parenthesis following the same process.
Let's put the a # on either side of ((a,b),(c,d)) to create our matrix:
You can now make the matrix as big as you would like with whatever numbers you like. For example, I can type this within two number signs ((-1,0,112),(0,-4,45),(-6,-6/5,-3)) to get:
I didn't want to alter Sally's excellent answer, so I posted this as a separate answer.
I want to show you some variations of the classic matrix format. You can write
- Without the hashtags
[ (x, y, z), (1, 2, 3), (4, 5, 6) ]
- With the hashtags
- Without the hashtags
| (x, y, z), (1, 2, 3), (4, 5, 6) |
- With the hashtags
- Without the hashtags
|| (x, y, z), (1, 2, 3), (4, 5, 6) ||
- With the hashtags
Found the last two while looking for ways to write definitions by cases :D
- Without the hashtags
{ (x, y, z), (1, 2, 3), (4, 5, 6) :}}
- With the hashtags
- Without the hashtags
{: (x, y, z), (1, 2, 3), (4, 5, 6) :}
- With the hashtags
Here's what I've got too.
Explanation:
Another type of brackets
(:(x,y,z),(a,b,c),(1,2,3):) or <<(x,y,z),(a,b,c),(1,2,3)>>
You can mix left and right sides independently (not including |)
[(x,y,z),(a,b,c),(1,2,3):)
{(x,y,z),(a,b,c),(1,2,3))
{:(x,y,z),(a,b,c),(1,2,3):}}
You can leave empty cells
((,y,),(a,,c),(,2,))
((x,,z),(,b,),(1,,3))
Nonsquare and nested matrices are also possible.



