How will you prove the formula #sin(A+B)=sinAcosB+cosAsinB# using formula of scalar product of two vectors?
1 Answer
As below
Explanation:
```````````````````````````````````````````````````````````````````````````````````````````````````````````````````
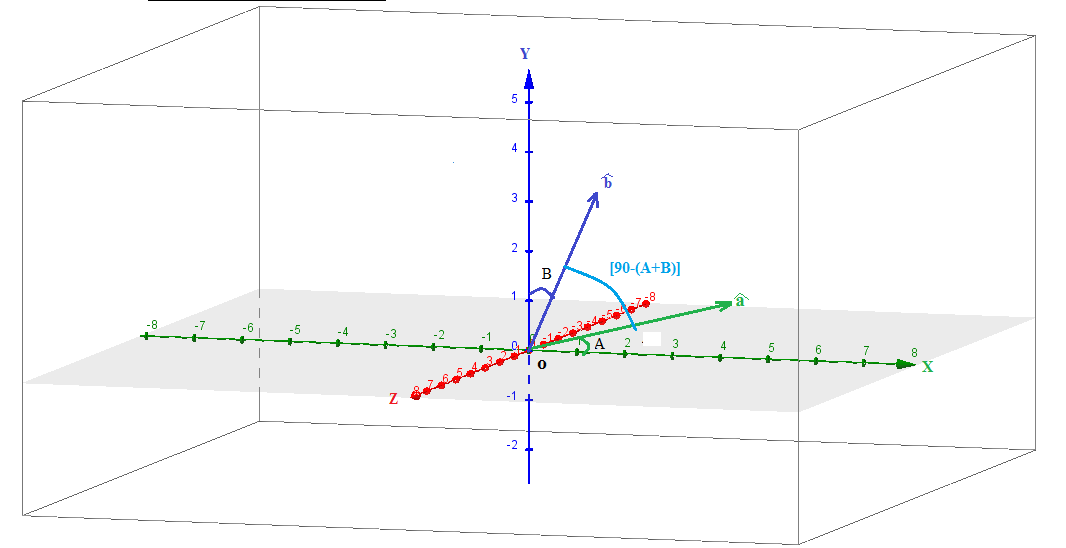
Let us consider two unit vectors in X-Y plane as follows :
#hata-># inclined with positive direction of X-axis at angles A# hat b-># inclined with positive direction of X-axis at angles 90-B, where# 90-B>A# - Angle between these two vectors becomes
#theta=90-B-A=90-(A+B)# ,
Now
Applying Properties of unit vectos
and
Also inserting
Finally we get
```````````````````````````````````````````````````````````````````````````````````````````````````````
Sin(A+B) =SinA CosB + CosASinB formula can also be obtained
by taking scalar product of
Now
Applying Properties of unit vectos
and
Also inserting
Finally we get

