How would you find the equations of both the horizontal and vertical asymptotes for the following functions: #y=(x)/(x-3)#? #y=(x+4)/(x^2-1)#? #y=(x+4)/(x^2-1)#? #y=(x^2-2x+1)/(x^2-3x-4)#? #y=(x^2-9)/(x^2-3x^2-18x)#?
In addition, how would you find the coordinates of any holes for these problems?
In addition, how would you find the coordinates of any holes for these problems?
3 Answers
vertical asymptote at x = 3
horizontal asymptote at y = 1
Explanation:
For y
#=x/(x-3)# The denominator of y cannot be zero as this is undefined. Equating the denominator to zero and solving gives the value that x cannot be and if the numerator is non-zero for this value then it is a vertical asymptote.
solve: x - 3 = 0
#rArrx=3" is the asymptote"# Horizontal asymptotes occur as
#lim_(xto+-oo),ytoc" (a constant)"# divide terms on numerator/denominator by x
#(x/x)/(x/x-3/x)=1/(1-3/x)# as
#xto+-oo,yto1/(1-0)#
#rArry=1" is the asymptote"#
graph{(x)/(x-3) [-10, 10, -5, 5]}
vertical asymptotes at x = ± 1
horizontal asymptote at y = 0
Explanation:
For
#y=(x+4)/(x^2-1)# The explanation for vertical/horizontal asymptotes is as described above in previous question.
solve:
#x^2-1=0rArr(x-1)(x+1)=0rArrx=±1#
#rArrx=-1" and " x=1" are the asymptotes"# To obtain horizontal asymptote divide terms on numerator/denominator by the highest power of x, that is
#x^2#
#(x/x^2+4/x^2)/(x^2/x^2-1/x^2)=(1/x+4/x^2)/(1-1/x^2)# as
#xto+-oo,yto(0+0)/(1-0)#
#rArry=0" is the asymptote"#
graph{(x+4)/(x^2-1) [-10, 10, -5, 5]}
For:
Explanation:
Start by factoring both the numerator and the denominator:
Nothing can get canceled out, so we don't have any holes. Now for asymptotes. The vertical asymptotes can be found by setting the denominator to
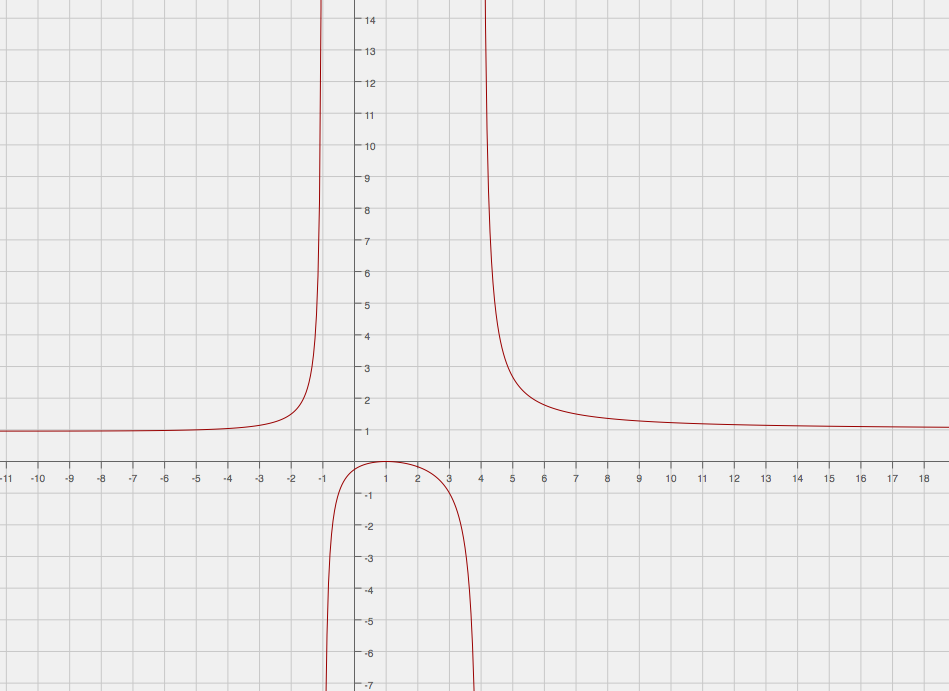
So, the equations of the vertical asymptotes will be
For the horizontal asymptotes, we must examine the degree of the denominator relative to that of the numerator.
•The denominator is of degree
•The numerator is of degree
When the degrees are equal, the horizontal asymptote occurs at the ratio between the coefficients of the highest degree in the numerator and in the denominator.
Hence,
So, there will be a horizontal asymptote at
In summary:
The graph of
Bonus:
Here is the graph of the function. As you can see, the asymptotes are just where algebra showed them to be.
Hopefully this helps!

