Question

How would you solve `sqrt(x+10)=-3`?

Answer 1

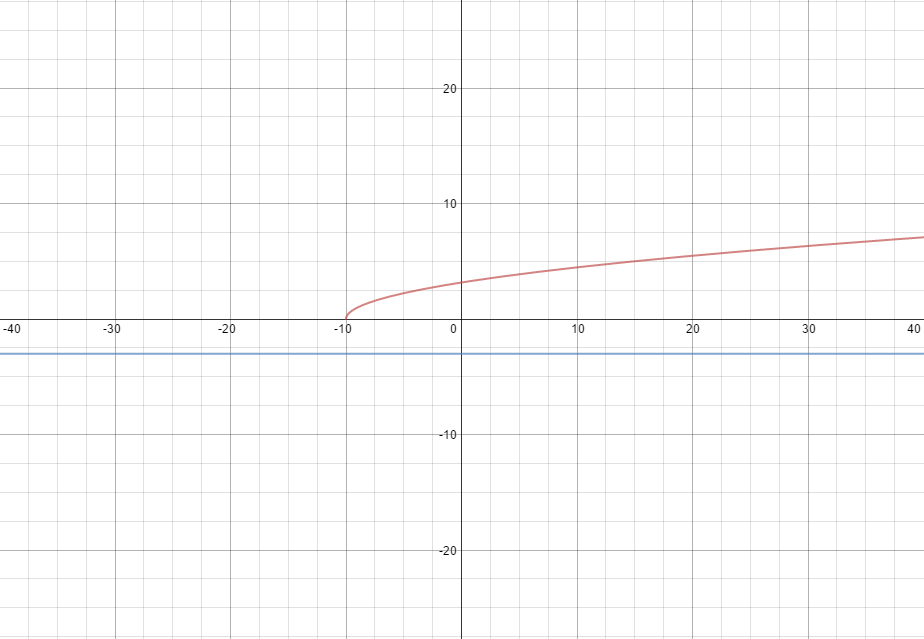
In the set of real numbers the equation `sqrt(10+x)=-3` has no solutions because the left part is always positive or equal to zero for `x=-10` and the right part is always negative.

If you see the graph of both functions `y=sqrt[x+10]` (red line) and `y=-3` (blue line)
it is apparent that no real solutions exist.

Answer 2

x = -1

Explanation:

Well

`sqrt(x+10) = -3`

Square both sides

`x +10= 9`

`x = -1`
So

`sqrt 9 = +-3`