Question

If `13/4 L` of a gas at room temperature exerts a pressure of `16 kPa` on its container, what pressure will the gas exert if the container's volume changes to `5/12 L`?

Answer 1

The gas will exert a pressure of `624/5 kPa`

Explanation:

Let's begin by identifying our known and unknown variables.

The first volume we have is `13/4`L, the first pressure is `16kPa` and the second volume is `5/12L`. Our only unknown is the second pressure.

We can obtain the answer using Boyle's Law:

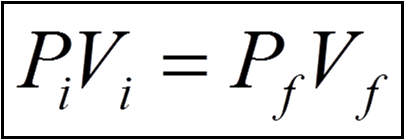
The letters i and f represent the initial and final conditions, respectively.

All we have to do is rearrange the equation to solve for the final pressure.

We do this by dividing both sides by `V_f` in order to get `P_f` by itself like so:
`P_f=(P_ixxV_i)/V_f`

Now all we do is plug in the values and we're done!

`P_f=(16\kPa xx 13/4\ cancel"L")/(5/12\cancel"L")` = `624/5kPa`