Question

If a projectile is shot at an angle of `(5pi)/12` and at a velocity of `15 m/s`, when will it reach its maximum height??

Answer 1

10.711 meters

Explanation:

Split the velocity up into x-components and y-components:

`vx=15cos(5pi/12)`

`vy=15sin(5pi/12)`

We only care about the y-component in this case since we want to know maximum height. The initial velocity is `15sin(5pi/12)`. The final velocity will be `0` at the top. The acceleration is always `9.8` m/s downwards. We need to find d. Find a kinematics equation that has `vi`, `vf`, `a`, and `d`.

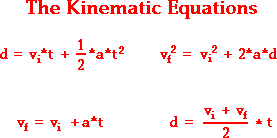
The equation in the top right corner has all four of those components. Plug into that equation:

`0=(15sin(5pi/12))^2+2(-9.8)(d)`

Solve for d:

`d=(-15sin(5pi/12))^2/((2)(-9.8))=10.711 m`