If a series–parallel circuit has all 30-ohm resistors, what is the total resistance when r1 is in series with a parallel circuit consisting of r2 and r3?
2 Answers
If a series–parallel circuit has all 30-ohm resistors, the total resistance when r1 is in series with a parallel circuit consisting of r2 and r3 is
Explanation:
Parallel circuit:
If two resistances are in parallel,then we can replace the parallel combination of two resistances by a single equivalent resistance which is equals to the ratio of the product of those resistance values to the summation of those resistance values.
The single equivalent resistance shows the same affect as the parallel combination.
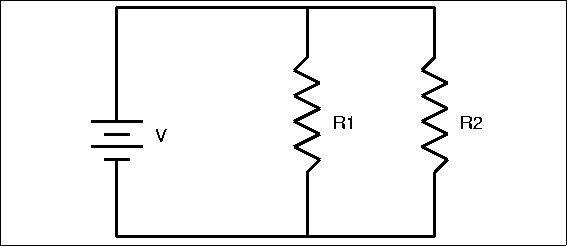
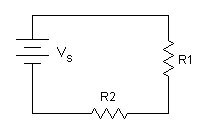
series circuit:
If two resistances are in series,then there is a chance to replace these two individual resistances by single equivalent resistance which is summation of both resistances values.
The single equivalent resistance drops the voltage which is same as the drop due to the combination of two individual resistors.
solution:
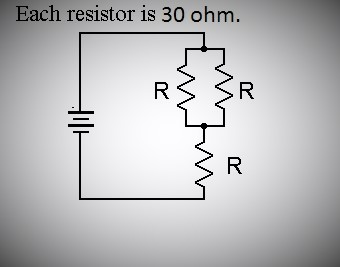
substitute
here R=30 ohms
In a series-parallel circuit of three identical resistors of any value you will find the total resistance will always be equal to the resistance of one resistor plus half again or 1.5 x R.
Explanation:
Two resistors of the same value in parallel will always result in half the value of either one.
When added to the series resistor of equal value the total resistance will be 1.5 x R.

