Question

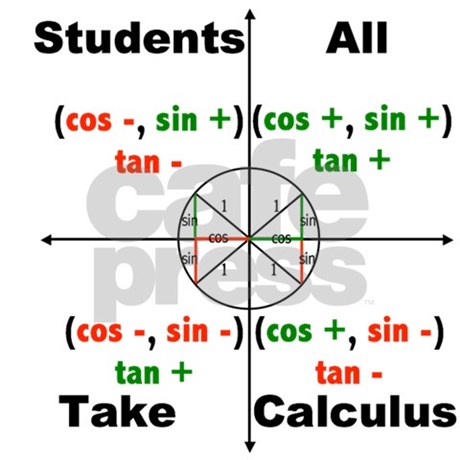
If cos >0 and sin <0 what quadrant is it in?

Answer 1

Consider the rule `C-A-S-T` or All Slow Turtles Crawl for this type of problem.

Both of these rules indicate in which quadrant the trigonometric function is positive. In all quadrants except the first, only 1 out of the three trigonometric functions are positive; the other two are negative.

Quadrant 1: All are positive
Quadrant 2: Sine is positive
Quadrant 3: Tangent is positive
Quadrant 4: Cosine is positive

The acronym and the expression mentioned above are meant to facilitate your ability to remember these. Beware, though that C-A-S-T starts in the 4th quadrant and then goes to the 1st, 2nd and finally the 3rd, while "All Slow Turtles Crawl# goes from 1st to 4th.

Now, back to the problem at hand.

If cosine is positive, then we are already limited to 2 quadrants: IV and I. However, in quadrant I, all the functions are positive, and the problem says that sin is negative in this case. This leaves us one option: quadrant IV.

Hopefully this helps!

Answer 2

`"Quadrant IV"`

Explanation:

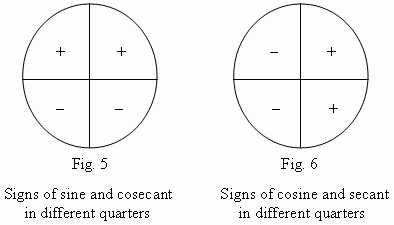
Cosine correlates with values of `x`.
Values of `x` are positive in `"Quadrant I"` and `"Quadrant IV"`.
Cosine is positive in the same quadrants.

Sine correlates with values of `y`.
Values of `y` are negative in `"Quadrant III"` and `"Quadrant IV"`.
Sine is negative in the same quadrants.

The only quadrant where `x` is positive, so `cos(x)>0`, and `y` is negative, so `sin(x)<0`, is `"Quadrant IV"`.

An example of an angle in `"Quadrant 4"` is `(7pi)/4`.

`cos((7pi)/4)=sqrt2/2>0`

`sin((7pi)/4)=-sqrt2/2<0`