Question

If IA+BI = IA-BI, find the angle between the vector A and B and show that the two vectos are perpendicular to each other. How to answer this question?

Answer 1

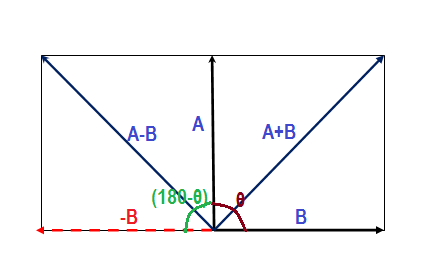
Let the angle between two vectors `A and B` be `theta`

So

`abs(A+B)^2=abs(A)^2+abs(B)^2+2abs(A)abs(B)costheta`

Again

`abs(A-B)^2=abs(A)^2+abs(B)^2+2abs(A)abs(B)cos(180-theta)`

By the given condition

`abs(A+B)=abs(A-B)`

So

`costheta=cos(180-theta)`

`=>theta=180-theta`

`=>theta=90^@`

Answer 2

See below.

Explanation:

Considering that `A ne 0` and `B ne 0`

If `norm(A+B)` = `norm(A-B)` then

`norm(A+B)^2` = `norm(A-B)^2` or

`normA^2+2<< A, B >> + normB^2= normA^2-2<< A,B >> +normB^2`

or simplifying

`<< A,B >> = 0`

This means that the scalar product of `A` and `B` is null so the two vectors are orthogonal, and the angle between then is obtained knowing that

`<< A,B >> = cos(hat(AB))normA normB`. Now supposing that `normA ne 0` and `norm B ne 0` we have

`cos(hat(AB)) = << A, B >> /(normA normB) = 0` so `hat(AB)=pi/2`

Answer 3

We can use some properties of the Vector Norm.

`||A|| = sqrt(A * A) => ||A||^2 = A * A`

We are given that:

`|| A+B || = || A - B||`

If we square both sides we get:

`|| A+B ||^2 = || A - B||^2`

Using the above property this becomes:

`(A+B) * (A+B) = (A - B) * (A-B)`

And the Vector Dot Product is distributive over vector addition so we can expand the above expression;

`(A+B) * A + (A+B) * B = (A - B) * A - (A - B) * B`
`:. A*A+B*A + A*B+B* B = A*A - B* A - A*B + B * B`
`:. B*A + A*B = - B* A - A*B`

And the vector product is Commutative so `A*B=B*A`;

`:. A*B + A*B = - A* B - A*B`
`:. 2A*B = -2 A* B`
`:. 4A*B = 0`
`:. A*B = 0`

And If `A*B=0` then either:

`A=0` or `B=0`; or
`A` and `B` are perpendicular. QED